«MEDIDAS DE TENDENCIAS CENTRALES
»
Prepara tus exámenes
Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity
Consigue puntos base para descargar
Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium
Orientación Universidad
Prepara tus exámenes
Prepara tus exámenes y mejora tus resultados gracias a la gran cantidad de recursos disponibles en Docsity
Busca documentos
Prepara tus exámenes con los documentos que comparten otros estudiantes como tú en Docsity
Busca documentos en el Store
Los mejores documentos en venta realizados por estudiantes que han terminado sus estudios
Video Cursos
Estudia con lecciones y exámenes resueltos basados en los programas académicos de las mejores universidades
Quiz
Responde a preguntas de exámenes reales y pon a prueba tu preparación
Consigue puntos base para descargar
Gana puntos ayudando a otros estudiantes o consíguelos activando un Plan Premium
Comunidad
Pregúntale a la comunidad
Pide ayuda a la comunidad y resuelve tus dudas de estudio
Ranking de las universidades
Descubre las mejores universidades de tu país según los usuarios de Docsity
Ebooks gratuitos
¡Nuestros e-books salva-estudiantes!
Descarga nuestras guías gratuitas sobre técnicas de estudio, métodos para controlar la ansiedad y consejos para la tesis preparadas por los tutores de Docsity
Medidas de tendencia, Diapositivas de Estadística
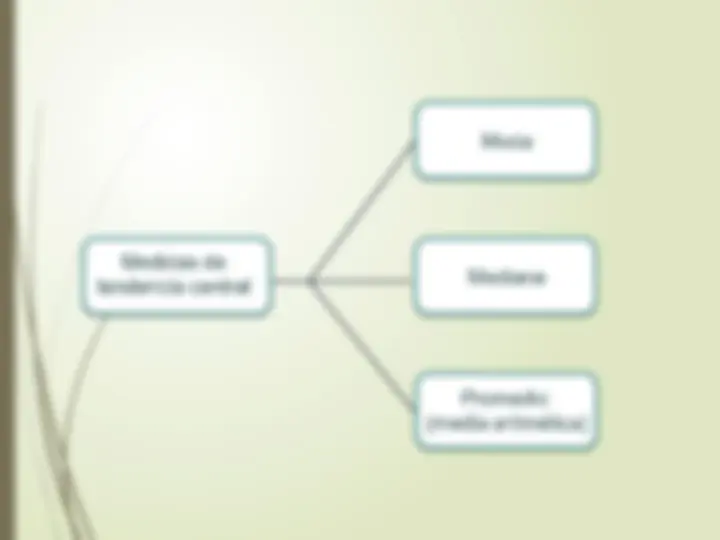
Tabla de medias de centralización
Tipo: Diapositivas
2024/2025
1 / 54
Esta página no es visible en la vista previa
¡No te pierdas las partes importantes!
Documentos relacionados
Vista previa parcial del texto
¡Descarga Medidas de tendencia y más Diapositivas en PDF de Estadística solo en Docsity!
« MEDIDAS DE TENDENCIAS CENTRALES
OBJETIVOS:
Calcular e interpretar las medidas de tendencia
central.
Aplicar la estadística descriptiva en
la resolución de problemas de la
vida real.
MODA
La moda de una serie de datos es aquel valor que se presenta con mayor
frecuencia, es decir, es el valor que más se repite. La moda puede no existir
(amodal) y si existe, puede no ser única. Ademas, se puede repetir mas de una
vez (multimodal: bimodal, trimodal, etc)
Ejemplo 1: En la siguiente serie de datos ¿cuál crees que es la moda?
9, 2, 5, 5, 10, 11, 2, 2, 17, 2
La moda es 2 , y su frecuencia es 4.
Ejemplo 2: ¿Cuál será la moda en la siguiente serie de datos?
1, 3, 11, 5, 3, 11, 1, 5, 18, 18
Todos los datos tienen igual frecuencia, por lo cual la muestra NO tiene moda.
A) MODA EN DATOS NO AGRUPADOS
Ejemplo: En la siguiente tabla de frecuencias, se presentan las
temperaturas mínimas registradas durante el mes de mayo en la
ciudad de Santiago.
¿Cuál fue la moda de las temperaturas mínimas registradas?
La moda es 5° y su
frecuencia es 9
B) MODA EN DATOS AGRUPADOS
El intervalo modal (o clase modal) corresponde al intervalo que tiene
la mayor frecuencia.
Ejempl
o:
En este caso, es [8 – 11].
Nota : Esto NO significa que en ese intervalo se encuentre la
moda
de la muestra.
Intervalo
modal
mayor
frecuencia
Obtengamos la moda en el
ejemplo anterior:
Mo = 8
16−
(16−0)∙(16−12)
Mo = 8
16
(16)∙(4)
Mo = 8 + 1 = 9
La moda es 9
años.
MEDIANA (O PERCENTIL 50)
Corresponde al valor central de todos los datos de una
muestra, ordenados en forma ascendente o
descendente.
Cuando la muestra presenta una cantidad par de
datos, la mediana corresponderá al promedio de los
dos datos centrales.
Ejemplo 1: Los puntajes de 8 alumnos son los
siguientes:
¿Cuál es la mediana de los puntajes?
Nota : La mediana se puede hallar solo para variables
Ejemplo 2:
¿Cuál será la mediana de las siguientes puntuaciones en un
juego?
120 – 114 – 189 – 120 – 107 – 150 – 132
Solución: Primero, ordenaremos los datos de menor a mayor.
Mediana o percentil 50 = 120
Nota : Como el total de datos es impar, la mediana es
solo el valor central
🞭.
Dato
central
MEDIANA EN DATOS AGRUPADOS
El intervalo donde se encuentra la mediana se determina
ubicando la posición central, de acuerdo a las frecuencias
acumuladas.
Ejemplo:
Como hay 49 datos en total, la mediana se encuentra en
la posición 25. Luego, el intervalo donde se encuentra la
mediana es [12 – 15].
Datos de
posición 17
al 28
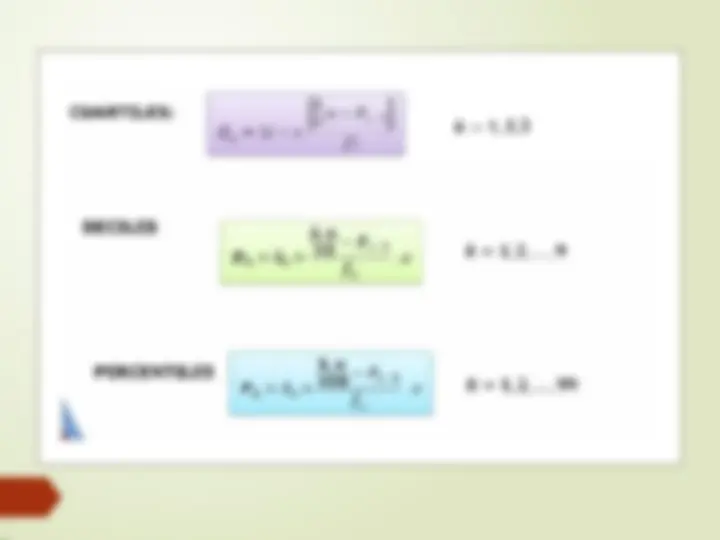
La forma que permite determinar la mediana para
datosagrupados
es:
𝑛
Me = 𝐿 𝑖
2
− 𝐹 𝑖− 1
𝑓 𝑖
∙ 𝐴
𝑖
Donde:
L i
: límite inferior del intervalo en el cual se encuentra la mediana.
n: número de datos del estudio. Es la sumatoria de las frecuencias absolutas.
F i-
: frecuencia acumulada del intervalo anterior al que se encuentra la mediana.
A i
: amplitud del intervalo en el que se encuentra la mediana.
f i
: frecuencia absoluta del intervalo en el que se encuentra la mediana.
PROMEDIO (O MEDIA ARITMÉTICA) (𝑥)
Es la suma de todos los datos, dividida por el número de
datos.
Ejemplo 1:
Los puntajes de 8 alumnos son los siguientes:
Luego, el promedio (o media aritmética) es:
x =
x = 640
Nota: El promedio se puede hallar solo para variables