¡Descarga apuntes de estatica en unidad 4 y 5 y más Apuntes en PDF de Estática solo en Docsity!
Unidad 4 Centroide y centro de gravedad
4.1 Generalidades
En el diseño estructural intervienen cuerpos de tres dimensiones y en ellos generalmente dos de las dimensiones constituyen la sección y la otra es la longitud; es entonces de suma importancia el conocimiento de las secciones y de sus propiedades.
Sección L
Las propiedades que estudiaremos en esta unidad son el centroide y el momento de inercia. El centroide es el centro del área de una sección y el momento de inercia ( I ) es una expresión matemática que se requiere determinar para realizar cálculos posteriores. Las figuras más comunes son:
4.2 Centro de gravedad de un cuerpo bidimensional
Consideremos una placa o lámina plana horizontal como se muestra en la figura. Z Y W X G y X
La placa puede dividirse en “n” elementos pequeños. Las coordenadas del primer elemento se representa con X 1 , Y 1 , las del segundo elemento con X 2 , Y 2. Etc. Las fuerzas ejercidas por la tierra sobre los elementos de la placa serán representados respectivamente con ∆W 1 , ∆W 2 , … ∆Wn Z Z y Y ∆W 1 W ∆W 2 X = X 1 G X 2 Y 1 Y Y 2 X X ∑My: X W = ∑ X ∆ W ∑Mx: Y W = ∑ Y ∆ W Estas fuerzas o pesos están dirigidos hacia el centro de la tierra; sin embargo, para todos los propósitos prácticos podemos suponerlos paralelos, entonces su resultante es una fuerza única en la misma dirección. La magnitud W de esta fuerza se obtiene sumando las magnitudes de las fuerzas elementales, ∑Fz: W = ∆W 1 + ∆W 2 + … Wn 1
Sustituyendo las ecuaciones 4 y 5 en las ecuaciones número 2 y dividiendo entre ℽ t, tenemos: ∑My: X ℽ t A/ ℽ t = X 1 ℽ t ∆A 1 / ℽ t + X 2 ℽ t ∆A 2 / ℽ t + … + Xn ℽ t ∆A n/ ℽ t
∑Mx: Y ℽ t A/ ℽ t = Y 1 ℽ t ∆A 1 / ℽ t + Y 2 ℽ t ∆A 2 / ℽ t + … + Yn ℽ t ∆A n/ ℽ t
Por lo tanto la ecuación queda: ∑My: X A = X 1 ∆A 1 + X 2 ∆A 2 + … + Xn ∆A n 6 ∑Mx: Y A = Y 1 ∆A 1 + Y 2 ∆A 2 + … + Yn ∆A n
Si aumentamos el número de elementos en que se subdivide el área, disminuyendo simultáneamente el tamaño de cada elemento, obtenemos el límite, entonces: X A = ʃ X dA 7 Y A = ʃ Y dA
Estas ecuaciones definen las coordenadas X, Y del centro de gravedad o centroide de una placa homogénea. El centroide o centro de gravedad de una sección cualquiera se define como el centro físico del área de dicha sección y se denota por la letra C. Las coordenadas del punto C son: C (x, y). También se puede representar como C (XC, YC); asimismo como C (X 0 , Y 0 ) ó como C (XG, YG). Las ecuaciones básicas que se aplican para determinar las fórmulas que se utilizan para el cálculo son las siguientes: XA = ʆ X dA YA = ʆ Y dA Con éstas ecuaciones se obtienen las fórmulas para calcular el centroide o centro de gravedad de figuras o secciones sencillas.
4.4 Centroides por integración
a) Centroide se una sección rectangular Ecuaciones básicas: XA = ʆ X dA YA = ʆ Y dA
Y dx dA = h dx
x h
0 X b
b b b b
XA = ∫X dA = ∫ X dA = ∫ X h dx = h ∫ X dx = h X^2 /2 = h b^2 /
XA = h b^2 / Y como A = b h, entonces, X b h = h b^2 /2, despejando X, tenemos: h b^2 /2 b X = ----------- = b /2 X = ------ b h 2
Y dA = b dy
dy h y 0 X b
b
XA = ∫X dA = ∫ X dA
b b b b h h h h XA = X ----- (b – X) dx = ----- X ( b – X) dx = ----- X b dx - ---- X^2 dx b b b b 0 0 0 0 b b b b h b h X^2 h X^3 hb^2 h b^3 = ----- X dx - ----- X^2 dx = h ----- - ----- ------ = ------- - ------- b b 2 b 3 2 b (3) 0 0 0 0 h b^2 h b^2 3 hb^2 - 2 hb^2 h b^2 = ------ - ------ = ---------------- = ------- 2 3 6 6 h b^2 b h XA = --------- y como A = ------, entonces: 6 2
b h h b^2 2 h b^2 b X ------- = ---------, entonces X = -------- = ---- 2 6 6 b h 3
b h X = ----- de manera análoga Y = ----- 3 3
Como observamos en la figura el X = XC = X 0 = XG, es la distancia que hay entre el centro del área C o centro de gravedad (CG) de la sección, al eje Y. El Y = YC = Y 0 = YG, es la distancia que hay entre el centro del área C o centro de gravedad (CG) de la sección, al eje X.
A continuación se muestran tablas con las fórmulas para calcular el centroide de secciones sencillas. Figura x = XG y = YG Área Triángulo rectángulo y h
. c
x b
b 3
h 3
b h A = 2
R ectángulo y
. c h
x b
b 2
h 2
A = b h
4.5 Cálculo de centroides en secciones sencillas
Ejemplos: 1.- Determinar el centroide de la sección rectangular mostrada en la figura.
30 cm
50 cm Se ponen los ejes de referencia.
Y X
. C 30 cm Y 50 cm X
XC = b/2 = 50 cm / 2 = 25 cm YC = h/2 = 30 cm / 2 = 15 cm Entonces C (25 cm, 15 cm)
Si cambiamos los ejes de referencia, tenemos:
Y
50 cm
. C 30 cm
X
25 cm
XG = 0 cm YG = h/2 = 30 cm/2 = 15 cm C (0 cm, 15 cm)
Si de nuevo cambiamos los ejes de referencia, tenemos: Y 20 cm 50 cm
30 cm
25 cm X
X = b/2 + 20 cm = 25 cm + 20 cm = 45 cm Y = h/2 +25 = 15 cm + 25 cm = 40 cm C (45 cm, 40 cm)
Y
X
. C 30 plg
60 plg
X = 1/3 b = 1/3 (60 plg) = - 20 plg (Valor negativo porque está a la izquierda del eje Y) Y = 2/3 h = 2/3 (30 plg) = - 20 plg (Valor negativo porque está abajo del eje X) C (-20 plg, - 20 plg)
3.- Determinar el centroide de la sección semicircular mostrada en la figura. Y
X
20 m
Xc = r = 10 m Yc = 4r/3π = 4(10)/3π = 4.24 m C (10 m, 4.24 m) Nota: Si cambiamos la posición de la figura, también cambia el valor de las coordenadas del centroide.
4.6 Cálculo de centroides en secciones compuestas
Si tenemos una sección compuesta, como la que se indica: Y
. C
X
Para calcular el centroide de éste tipo de secciones, se procede como sigue: 1).- Se divide la figura en secciones sencillas como son: rectángulos, triángulos, círculos, semicírculos, etc.; como se indica a continuación: Y
X
2).- Se numeran las figuras y se determina el centroide de cada sección sencilla, como se indica:
Y 1 2. C
. C 3. C X
Y
9 plg 6 plg
X 6 plg 1.- Dividiendo la sección en figuras sencillas.
Y
3 plg
6 plg 6 plg
X 6 plg
2).- Numerando las figuras y determinando su centroide.
Y X 1 = 2 plg
. C 1 . C 2 Y1 = 7 plg Y 2 = 3 plg X X 2 = 3 plg
3).- Tabla de cálculo
Componente Área (Plg^2 )
_
X (Plg)
_
Y (plg)
_
XA (Plg^3 )
_
YA (Plg^3 ) 1 9 2 7 18 63 2 36 3 3 108 108 ∑ = 45 (Plg^2 ) 126 (Plg^3 ) 171 (Plg^3 )
- Cálculo del centroide de la figura
X = ∑XA / ∑ A = 126 (Plg^3 ) / 45 (Plg^2 ) = 2.8 plg Y = ∑ YA / ∑ A = 171 (Plg^3 ) / 45 (Plg^2 ) = 3.8 plg C (2.8 plg , 3.8 plg)
Ejemplo 2.- Determinar el centroide o centro de gravedad de la sección T mostrada en la figura:
Y X 1 = 45 cm
1. C
. C Y 1 = 80 cm 2 Y 2 =30 cm X X 2 = 45 cm
3).- Tabla de cálculo
Componente Área (Cm^2 )
_
X (Cm)
_
Y (Cm)
_
XA (Cm^3 )
_
YA (Cm^3 ) 1 3600 45 80 162000 288000 2 1800 45 30 81000 54000 ∑ = 5400 (Cm^2 ) 243000 (Cm^3 ) 342000 (Cm^3 )
- Cálculo del centroide de la figura
X = ∑XA / ∑ A = 243000 (Cm^3 ) / 5400 (Cm^2 ) = 45 cm Y = ∑ YA / ∑ A = 342000 (Cm^3 ) / 5400(Cm^2 ) = 63.33 cm C (45 cm, 63.33 cm)
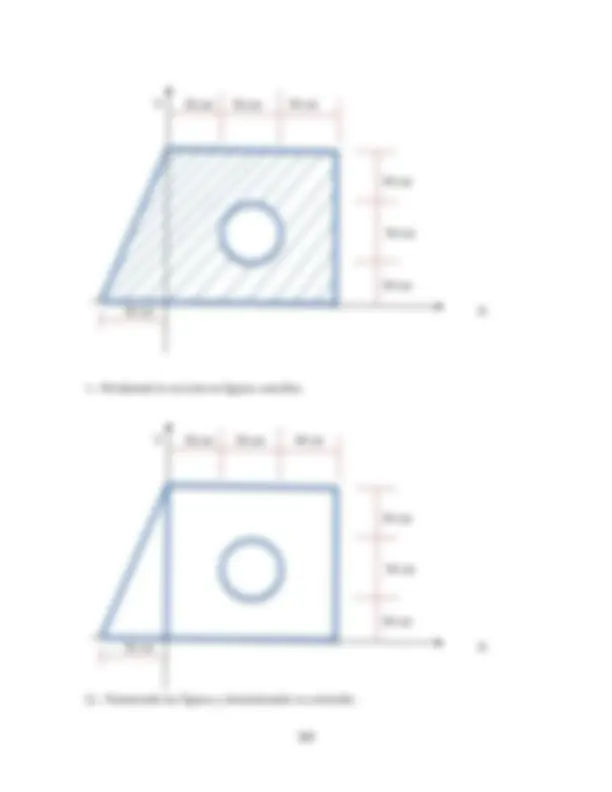
Ejemplo 3.- Determinar el centroide o centro de gravedad de la sección mostrada en la figura:
Y 30 cm 30 cm 30 cm
30 cm
30 cm
30 cm 36 cm X
1.- Dividiendo la sección en figuras sencillas.
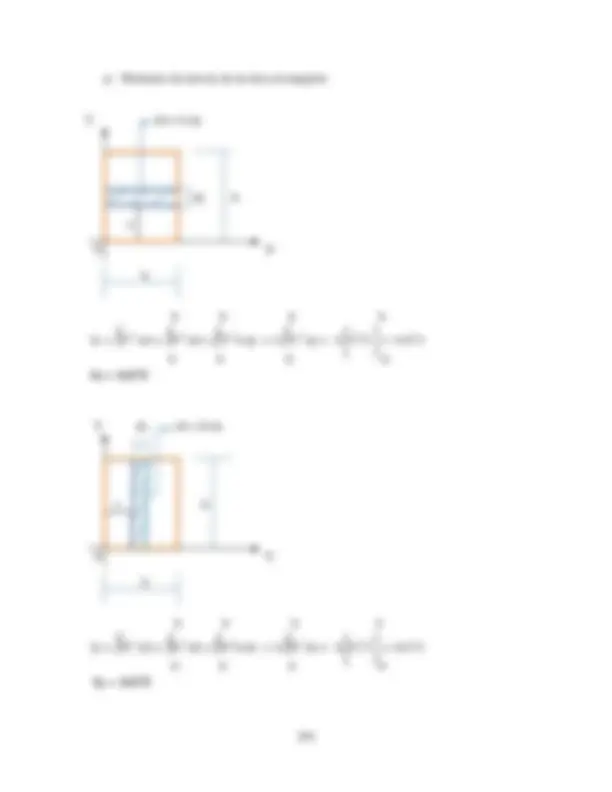
Y 30 cm 30 cm 30 cm
30 cm
30 cm
30 cm 36 cm X
2).- Numerando las figuras y determinando su centroide.
