APPLICATIONS
VOLUME BY INTEGRATION
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Guidelines and tips
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community
Ask the community for help and clear up your study doubts
University Rankings
Discover the best universities in your country according to Docsity users
Free resources
Our save-the-student-ebooks!
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Volume by Integration, Lecture notes of Engineering Mathematics
The concept of solid of revolution and the methods to calculate its volume. It describes the Ring or Washer method, which is used when the element is perpendicular to but not touching the axis. It also explains the Shell method, which is used when the element is parallel to the axis of revolution. an example of finding the volume of a solid generated by revolving the second quadrant region bounded by the curve about R =1-x using the Ring or Washer method.
Typology: Lecture notes
2021/2022
1 / 8
This page cannot be seen from the preview
Don't miss anything!
Related documents
Partial preview of the text
Download Volume by Integration and more Lecture notes Engineering Mathematics in PDF only on Docsity!
APPLICATIONS
VOLUME BY INTEGRATION
A solid of revolution is the figure formed when a plane region is revolved
about a fixed line. The fixed line is called the axis of revolution. For short,
we shall refer to the fixed line as axis.
The volume of a solid of revolution may be using the following
methods:
DISK, RING and SHELL METHOD
DISK METHOD: V = r
2
h
Find the volume of the solid generated by revolving the region bounded by the
line y = 6 – 2x and the coordinate axes about the y-axis.
r =x
( x , y )
h = dy
( 0 , 6 )
x
y
0
(3,0)
𝑉 =
0
6
𝜋 𝑥
2
𝑑𝑦
𝑉 =
0
6
𝜋
[
1
2
]
2
𝑑𝑦
𝑉 =
𝜋
4
0
6
( 6 − 𝑦 )
2
𝑑𝑦
( 6 − 𝑦 )
3
|
0
3
𝑥=
1
2
( 6 − 𝑦
)
𝑖𝑓 𝑦 = 6 − 2 x ;
𝑉 = −
𝜋
12
[
( 6 − 6
)
3
−
( 6 − 0
)
3
]
V r h
2
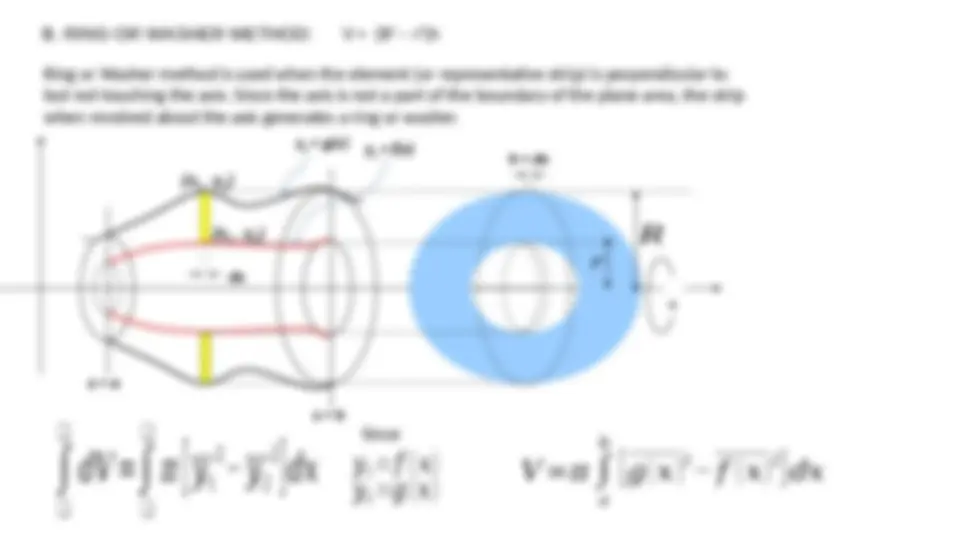
Ring or Washer method is used when the element (or representative strip) is perpendicular to
but not touching the axis. Since the axis is not a part of the boundary of the plane area, the strip
when revolved about the axis generates a ring or washer.
B. RING OR WASHER METHOD: V = (R
2
- r
2
)h
( x
1
, y
1
)
( x
2
, y
2
)
x = a
x = b
dx
h = dx
y
1
= g(x)
y
2
= f ( x )
❑
❑
𝑑𝑉 =
❑
❑
𝜋
[
𝑦
1
2
− 𝑦
2
2
]
𝑑𝑥
Since
𝑦
1
= 𝑓 (𝑥)
𝑦
2
=𝑔 (𝑥)
𝑉 =𝜋
𝑎
𝑏
[ 𝑔 ( 𝑥 )
2
− 𝑓 ( 𝑥 )
2
] 𝑑𝑥
r
R
C. SHELL METHOD:
The method is used when the
element (or representative strip) is
parallel to the axis of revolution.
When this strip is revolved about
the axis, the solid formed is of
hollow cylindrical form.
𝑉
𝑠 𝑒𝑙𝑙 h
= 2 𝜋 𝑟𝑡 ⋅ h
SHELL METHOD:
Find the volume of the solid generated by revolving the second quadrant region bounded
by the curve about the line.
𝒙
𝟐
= 𝟒 − 𝒚
𝑑𝑉 = 2 𝜋 ( 1 − 𝑥 ) 𝑦𝑑𝑥
𝑉 = 2 𝜋 𝑟 𝑡 h
𝑉 = 2 𝜋
− 2
0
( 1 − 𝑥 ) 𝑦 𝑑𝑥
0
− 2
0
− 2
but x
2
= 4 − 𝑦 ; y =4− x
2
0
− 2
[
( 4 − 𝑥
2
) − 𝑥
( 4 − 𝑥
2
) ] 𝑑𝑥
0
− 2
( 4 − 4 𝑥 − 𝑥
2
3
) 𝑑𝑥
𝑉 =
56 𝜋
3
𝑐𝑢. 𝑢𝑛𝑖𝑡𝑠