Vetores: Conceitos, Operações e Aplicações - Notas de Aula, Summaries of Analytical Geometry

Download Vetores: Conceitos, Operações e Aplicações - Notas de Aula and more Summaries Analytical Geometry in PDF only on Docsity!

Universidade Federal do Rio Grande do Norte

Escola de Ciências e Tecnologia

Vetores

Cap. 12, James Stewart e Thomas

Jefferson Soares da Costa

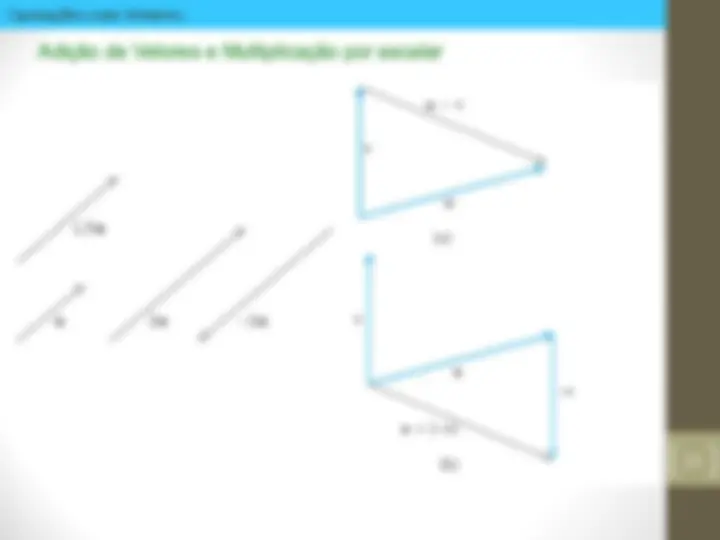
Grandezas Escalares: Caracterizadas por um número e uma unidade de medida: Ex. Massa, Comprimento, tempo. 1 kg, 10 m, 15 s. Grandezas Escalares e Vetoriais Grandezas Vetoriais: Caracterizadas por três características: Módulo, direção e sentido, além de uma unidade de medida: Ex. Deslocamento, velocidade, força.

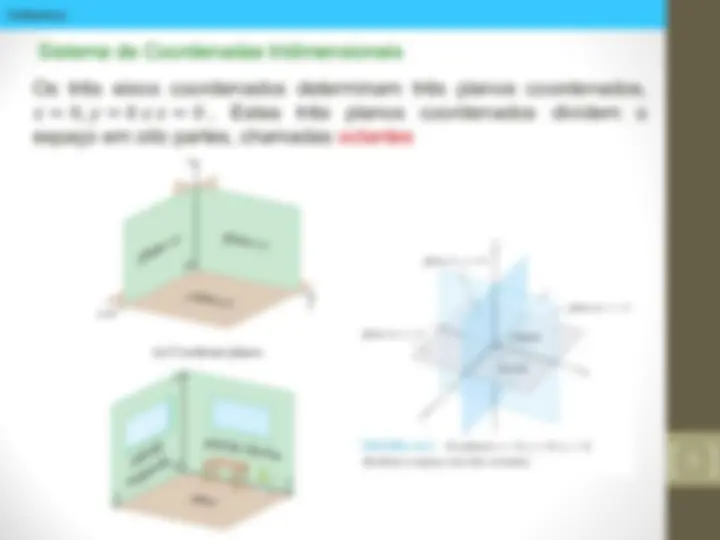
4 Representaremos qualquer ponto no espaço pela tripla ordenada (a, b, c) de números reais. Para representarmos os pontos no espaço (é um subconjunto do chamado ℝ " ), primeiro escolhemos um ponto fixo O (a origem) e três retas orientadas, estas são denominadas de eixos coordenados e chamdas de por eixo x, eixo y e eixo z Sistema de Coordenadas tridimensional Regra da mão direita

Os três eixos coordenados determinam três planos coordenados, ! = 0 , % = 0 ' ( = 0 , Estes três planos coordenados dividem o espaço em oito partes, chamadas octantes Sistema de Coordenadas tridimensionais

Localize os pontos no (– 4 , 3 , – 5 ) e ( 3 , – 2 , – 6 ) Exemplo 01 Solução

O produto cartesiano ℝ×ℝ×ℝ = {(&, (, ))|&, (, ) ∈ ℝ} é o conjunto de todas as triplas ordenadas de números reais que é denominado ℝ . . Na geometria analítica bidimensional, o gráfico de uma equação envolvendo x e y uma curvaem ℝ /

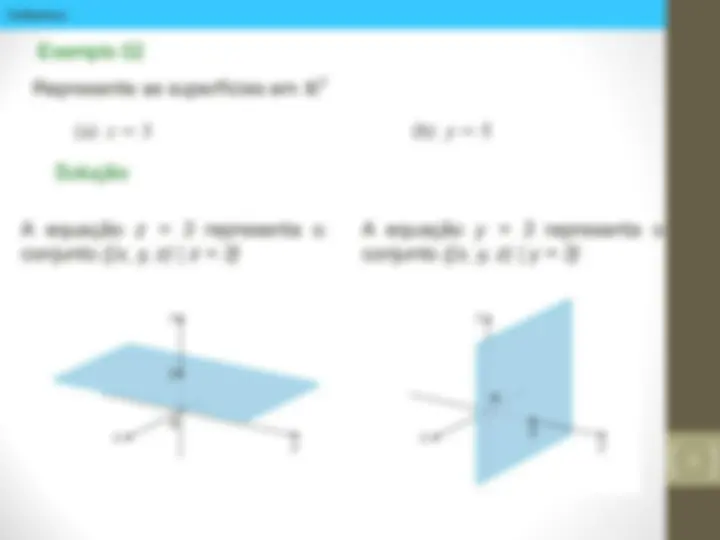
. Em geometria analítica tridimensional, uma equação em x, y e z representa uma superfície em ℝ . . Sistema de Coordenadas tridimensionais

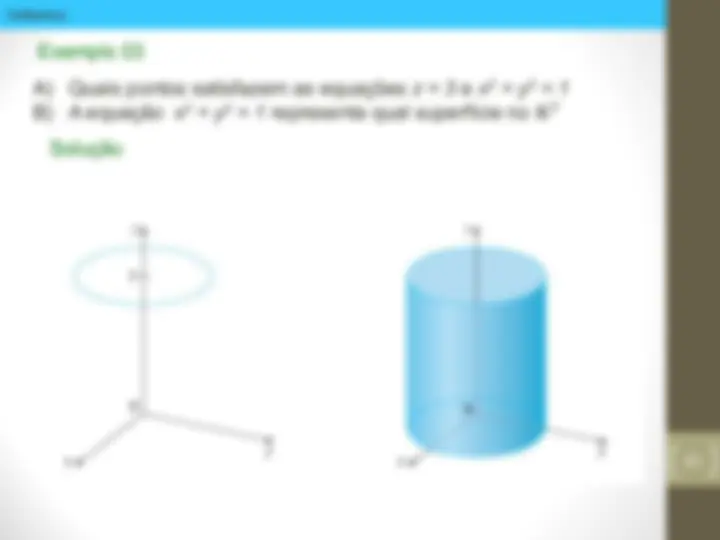
A) Quais pontos satisfazem as equações z = 3 e _x 2

• y 2 = 1_ B) A equação _x 2
• y 2 = 1_ representa qual superfície no ℝ " Exemplo 03 Solução

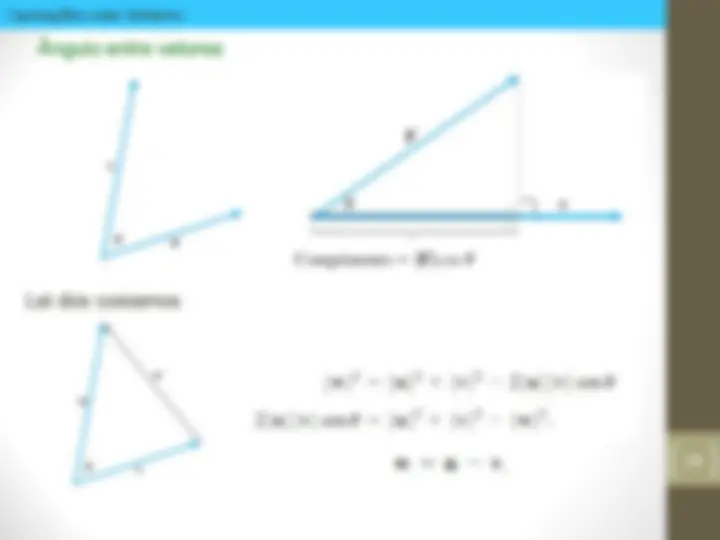
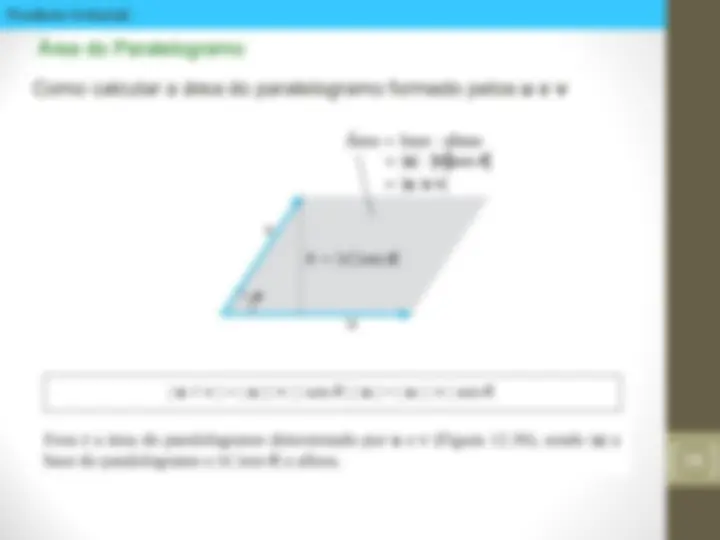
Distancia entre dois pontos Como calcular a distância entre dois pontos P 1 e P 2

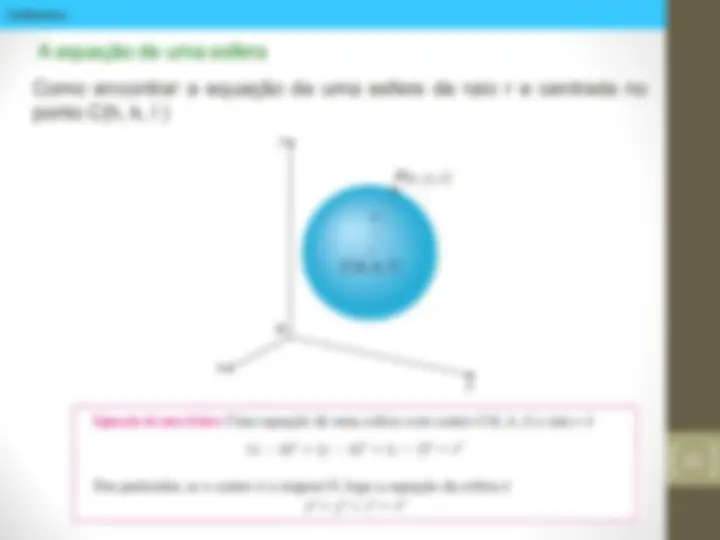
A equação de uma esfera Como encontrar a equação de uma esfera de raio r e centrada no ponto C(h, k, l )

Encontre o centro e o raio da esfera Exemplo 05 Solução Logo a esfera é centrada no ponto ( 1 , 2 , - 4 ) e possui raio r = 2

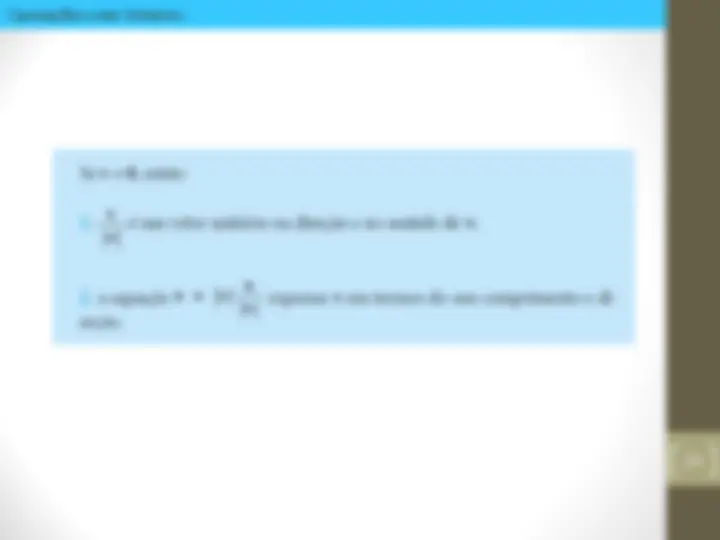
Componentes de um vetor

Vetores Unitários

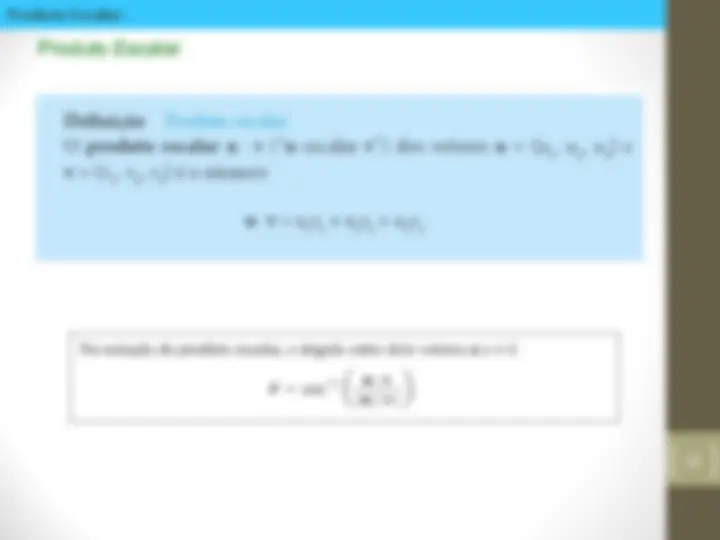
Encontre a) as componentes e b) o comprimento do vetor com ponto incial P = (- 3 , 4 , 1 ) e ponto final (- 5 , 2 , 2 ). Exemplo 06 Solução A)

Exemplo 06 Solução B)