Prepare for your exams
Get points
Guidelines and tips

Prepare for your exams

Study with the several resources on Docsity

Earn points to download

Earn points by helping other students or get them with a premium plan

Guidelines and tips

Sell on Docsity

Prepare for your exams

Study with the several resources on Docsity

Find documents

Prepare for your exams with the study notes shared by other students like you on Docsity

Search Store documents

The best documents sold by students who completed their studies

Search through all study resources

Docsity AINEW

Summarize your documents, ask them questions, convert them into quizzes and concept maps

Explore questions

Clear up your doubts by reading the answers to questions asked by your fellow students

Earn points to download

Earn points by helping other students or get them with a premium plan

Share documents

20 Points

For each uploaded document

Answer questions

5 Points

For each given answer (max 1 per day)

All the ways to get free points

Get points immediately

Choose a premium plan with all the points you need

Study Opportunities

Choose your next study program

Get in touch with the best universities in the world. Search through thousands of universities and official partners

Community

Ask the community

Ask the community for help and clear up your study doubts

University Rankings

Discover the best universities in your country according to Docsity users

Free resources

Our save-the-student-ebooks!

Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors

From our blog

Exams and Study

Go to the blog

Velocity analysis, Study Guides, Projects, Research of Physics

Heythrop College, University of London Physics

This method is useful in drawing the velocity diagram and finding the relative velocities of points on a link. • Let the velocity of B w.r.t A be represented by.

Typology: Study Guides, Projects, Research

2021/2022

Uploaded on 09/27/2022

christopher1 🇬🇧

4.5

(4)

222 documents

1 / 33

This page cannot be seen from the preview

Don't miss anything!

Velocity analysis

•To determine the velocities of different points

on links of a mechanism for a given input

motion. Determination of the motion

characteristics of links in a mechanism is

required for the force analysis

•

Velocities of links and of points of mechanism

•

Velocities of links and of points of mechanism

can be determined by different methods.

1. Relative velocity method or velocity polygon

method

2. Instantaneous centre method.

Partial preview of the text

Download Velocity analysis and more Study Guides, Projects, Research Physics in PDF only on Docsity!

Velocity analysis

-^ To determine the velocities of different pointson links of a mechanism for a given inputmotion. Determination of the motioncharacteristics of links in a mechanism isrequired for the force analysis •^ Velocities of links and of points of mechanism•^ Velocities of links and of points of mechanism^ can be determined by different methods.^ 1. Relative velocity method or velocity polygonmethod2. Instantaneous centre method.

Velocity of link

-^ In order to determine the relative motion ofthe ends of a link, one of the ends isassumed to be moving relative to the otherend. •^ Let a link

AB^ rotate about

A^ in anti-clockwise

direction such that the end

B^ rotates relative

A

direction such that the end

B^ rotates relative

to^ A. • Then the direction of relative motion of

B

with respect to

A^ is perpendicular to

AB.

-^ Therefore, the direction of relative velocity ofa point w.r.t any other point on a link isalways along perpendicular to the straightline joining the two points.

B

Velocity of link…

•^ Hence, the point

c^ divides the vector

ab^ in the

same ratio as the point

C^ divides the link

AB.

Relative velocity method

Velocity of any point on a link: Consider a link

AB^ where the directions

of motion of its ends are shown. Thevelocity vectors are shown. oa^ – velocity of the end

A

ob -^ velocity of the end

B^

A^ V C

A VB

ob -^ velocity of the end

B

ab - velocity of B with respect to

A

ba - velocity of A with respect to

B

B o^

a b^ c

Velocity diagram for four bar chain b

a, d

(i)

b^

(i)^ Draw a vector

ab^ perpendicular to the

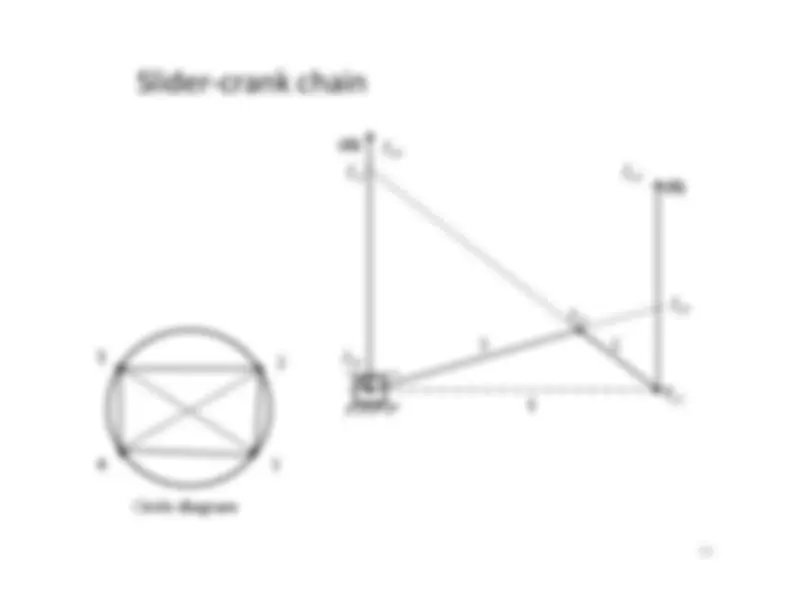
Given the dimensions of al l the links,angular velocity of the crank AB andposition of the crank. Draw configurationdiagram.

C B θ

a, d

b

(ii)^ a, d

b^ c

(iii)

(i)^ Draw a vector

ab^ perpendicular to the

link^ AB^

of length

AB x ω

(to a suitable

scale).(ii) Draw a vector line through

b^ in

direction perpendicular to the link

BC.

(iii) Draw a vector through d in a directionperpendicular to the link

CD.^ This will

intersect the vector through in

c.

(iv) The vector

bc^ represents velocity of

point C w.r.t point B.

Slider crank chain

o

a (i)^ a^

a^ c

Given the dimensions of al l the links, angular velocity ofthe crank OA and position of the crank. Drawconfiguration diagram.

A^ O

ω C

o^

(ii)

o

a^ b (iii)

o^

b

(i)^ Draw a vector

oa^ of length OA X

ω^ (taking a

suitable scale) in a direction perpendicular to OA. (ii) Draw a vector line through a in a directionperpendicular to the link

AB. (draw some length on either side of

a .)

(iii) Draw the vector ob parallel to

OB^ to intersect

the vector

ab^ at^ b. (iv) Divide the ab vector such that

ac : ab^ =^ AC

: AB^8

-^ Since no component of the velocity of the crank pin is used tomove the slider, whole the velocity of the crank at crank pinwill be used to move the lever and hence, the velocity of leverand velocity of tool at these positions (B

, B) are 34

maximum(neglecting obliquity of link CD). • Maximum velocity of cutting = maximum velocity of C whencrank pin is at B

Questions

1.For an inline slider-crank mechanism, the length of thecrank and connecting rod are 3 m and 4 m, respectively. Atthe instant when the connecting rod is perpendicular to thecrank, if the velocity of the slider is 1 m/s, the magnitude ofangular velocity (upto 3 decimal points accuracy) of the crankis _________radian/s.

Solution:

o 90 A^ O

o a

b^90

θ θ

3 m 4 m 5 m

m/s

Solution:^ OA x ω=0.8 m/s^ ω=0.8/3=0.2667 rad/s

A slider-crank mechanism with crank radius60 mm and connecting rod length 240 mm isshown in figure. The crank is rotating with auniform angular speed of 10 rad/s, counterclockwise. For the given configuration, the^ speed (in m/s) of the slider is _______speed (in m/s) of the slider is _______

1. For the four-bar linkage shown in the figure, theangular velocity of link AB is 1 rad/s. The length oflink CD is 1.5 times the length of link AB. In theconfiguration shown, the angular velocity of linkCD in rad/s is(A)
- (B) 3/
- (C)
- (D) 2/
  - Sol:Equal velocitiesAB x1 =CD x ωω=AB/CD=2/

For the configuration shown, the angular velocity oflink AB is 10 rad/s counterclockwise. The magnitude ofthe relative sliding velocity (in ms

-1) of slider B with

respect to rigid link CD is(A) 0^

(B) 0.

(D) 2.

Solution: From the dimension given,From the dimension given, angle ABC =

o velocity of crank at B = velocity of slider as AB isperpendicular to CDTherefore velocity of slider along CD =AB x 10 rad/s

=250 mm x10 rad/s = 2500 mm/s = 2.5 m/s

Answer : (D) 2.

Instantaneous center of rotation

-^ A link AB has moved

from A

Btooo^

AB. Its motion can be considerednn to have taken place in a number ofinfinitesimally small steps as shownin the figure. • Its motion from A

Bto Aoo^

Bcan be 11

considered as a pure rotation about a centre I. the location of the centre

Bo Bn

B^1

I

a centre I. the location of the centre can be obtained from direction ofthe velocities of the ends of the linkas shown. Such centre is called instantaneous centre of rotation

The location of the centre changesfrom instant to instant for differentpositions of the link and locus ofthese centres is called

centrode

Ao An

A^1

Where C is any point on the link.The angular velocities of various links can bedetermined easily using the above equation. Hence, the instantaneous centre method is simpler Hence, the instantaneous centre method is simpler than relative velocity method. than relative velocity method. when the directions are parallel , it becomes difficultto apply the method. But, relative velocity method issuitable for any configuration.

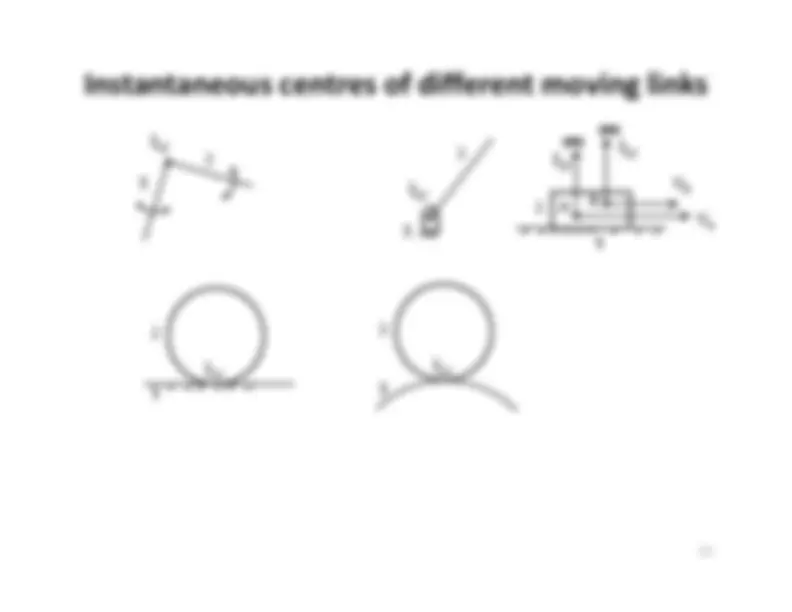
Instantaneous centres of different moving links^1

I^122

(^2) I (^121)

B^ A

VB 2

VA I^12 I^121

2 I^121

Velocity analysis, Study Guides, Projects, Research of Physics

Related documents

Partial preview of the text

Download Velocity analysis and more Study Guides, Projects, Research Physics in PDF only on Docsity!

Velocity analysis

Velocity of link

AB^ rotate about

A^ in anti-clockwise

direction such that the end

B^ rotates relative

A

direction such that the end

B^ rotates relative

to^ A. • Then the direction of relative motion of

B

with respect to

A^ is perpendicular to

AB.

B

Velocity of link…

•^ Hence, the point

c^ divides the vector

ab^ in the

same ratio as the point

C^ divides the link

AB.

Relative velocity method

AB^ where the directions

of motion of its ends are shown. Thevelocity vectors are shown. oa^ – velocity of the end

A

ob -^ velocity of the end

B^

ob -^ velocity of the end

B

ab - velocity of B with respect to

A

ba - velocity of A with respect to

B

Velocity diagram for four bar chain b

a, d

(i)

b^

(i)^ Draw a vector

ab^ perpendicular to the

a, d

b

(ii)^ a, d

b^ c

(iii)

(i)^ Draw a vector

ab^ perpendicular to the

link^ AB^

of length

AB x ω

(to a suitable

scale).(ii) Draw a vector line through

b^ in

direction perpendicular to the link

BC.

(iii) Draw a vector through d in a directionperpendicular to the link

CD.^ This will

intersect the vector through in

c.

(iv) The vector

bc^ represents velocity of

point C w.r.t point B.

Slider crank chain

o

a (i)^ a^

a^ c

o^

(ii)

o

a^ b (iii)

o^

b

, B) are 34

maximum(neglecting obliquity of link CD). • Maximum velocity of cutting = maximum velocity of C whencrank pin is at B

Questions

Solution:^ OA x ω=0.8 m/s^ ω=0.8/3=0.2667 rad/s