Unsteady Fluid Flow: Tank Discharge Calculations, Slides of Hydraulics

Download Unsteady Fluid Flow: Tank Discharge Calculations and more Slides Hydraulics in PDF only on Docsity!

UNSTEADY FLOW

Fluid Flow Measurement

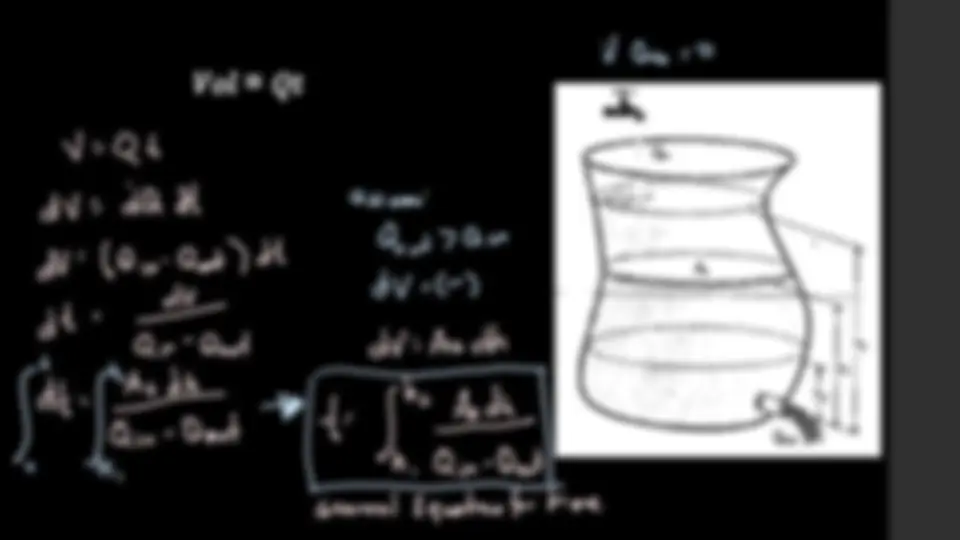
Where: Vol – volume of the liquid Q – the discharge which is constant or steady t – time for the liquid to flow

𝑡 = න ℎ 1 ℎ 2 𝐴 𝑠 𝑑ℎ 𝑄 𝑖𝑛 − 𝑄 𝑜𝑢𝑡 t is the time to lower the level from h 1 to h 2 assuming Q out

> Q

in 𝑡 = න ℎ 1 ℎ 2 𝐴 𝑠 𝑑ℎ 𝑄 𝑜𝑢𝑡 Interchanging the sign and Q in

𝑡 = 2 𝐴 𝑠 𝐶𝐴 𝑜 2 𝑔 ( 𝐻 1 − 𝐻 2 ) t is the time for the head to change from H 1 to H 2

𝑡 = 2 𝐴 𝑠 𝐶𝐴 𝑜 2 𝑔 න 𝐻 2 𝐻 1 𝐴 𝑠 1 𝐴 𝑠 2 𝐴 𝑠 1

• 𝐴 𝑠 2 𝐻 − ൗ 1 (^2) 𝑑𝐻 If liquid flows through a submerged orifice or tube connecting two tanks: If A s 1 and A s 2 are constant, i.e. the two tanks have uniform cross-sectional area: 𝑡 = 𝐴𝑠 1 𝐴𝑠 2 𝐴𝑠 1 + 𝐴𝑠 2 ( 2 𝐶𝐴𝑜 2 𝑔 ) ( 𝐻 1 − 𝐻 2 )

1 ) A 1. 5 - meter diameter vertical cylinder tank 3 m high contains 2. 5 m of water. A! 00 - mm diameter circular sharp- edged orifice is located at the bottom. Assume C = 0. 60. a. How long will it take to lower the water level to 1 m deep after opening the orifice? b. How long will it take to empty the tank?