ENGI 2102 Thermo-Fluid Engineering I
Chapter 2: Fluid Statics
G. Mazzanti
Process Engineering and Applied Science
Dalhousie University
Fall 2019
Slides by Michele Hastie, 2016
Slide 13 (page 31): Added diagram
Added Slide 28
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Guidelines and tips
Prepare for your exams
Study with the several resources on Docsity
Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community
Ask the community for help and clear up your study doubts
University Rankings
Discover the best universities in your country according to Docsity users
Free resources
Our save-the-student-ebooks!
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Fluid Statics: Pressure, Buoyancy, and Tank Failures, Slides of Thermodynamics
Thermofluids Notes on Fluid Statics and Work and Heat.
Typology: Slides
2020/2021
1 / 28
This page cannot be seen from the preview
Don't miss anything!
Related documents
Partial preview of the text
Download Fluid Statics: Pressure, Buoyancy, and Tank Failures and more Slides Thermodynamics in PDF only on Docsity!
ENGI 2102 Thermo-Fluid Engineering I
Chapter 2: Fluid Statics
G. Mazzanti
Process Engineering and Applied Science
Dalhousie University
Fall 2019
Slides by Michele Hastie, 2016
Slide 13 (page 31): Added diagram
Added Slide 28
Outline
2.1 Pressure
2.2 Pressure-Elevation Relationships
2.2.1 Constant Density
2.2.2 Isothermal, Perfect Gas
2.2.3 Isentropic, Perfect Gas
2.3 Manometers
2.4 Buoyancy and Stability
2.5 Hydrostatic Forces of Submerged Surfaces
2.6 Tank Failures
2.7 Problems
We will not cover
this section.
2.1 Pressure (page 26)
Pressure – the effect of a
normal force acting on an area
When a force Δ F acts at an
angle to an area Δ A it is only
the normal component Δ Fn
that is used to define pressure:
Common units of pressure:
101325 Pa = 101.325 kPa = 1.01325 bar = 1 atm = 14.696 psi
= 760 mmHg
A
F P
n
A (^)
→ 0
lim
2.1 Pressure (page 26)
Absolute pressure scale:
Relative to pressure in a perfect
vacuum
Gauge pressure scale:
Relative to atmospheric pressure
It is often more convenient to
measure values in gauge
pressure.
Calculations:
Most calculations require absolute
pressure ( e.g ., ideal gas law).
When calculating a change in
pressure, either gauge or absolute
pressure can be used ( e.g .,
pressure-depth equation).
Pabs = Patm + Pgauge
2.2 Pressure-Elevation Relationships (page 28)
Consider a small volume
(Δ x Δ y Δ z ) in a large mass
of fluid at rest.
Since the fluid is at rest, the sum of all the forces must be
zero.
Force balance in the z - direction:
Dividing by Δ x Δ y Δ z :
( Pz (^) = 0 ) x y −( Pz = z ) x y = g x y z
g
z
Pz (^) z Pz = −
= −^ = 0 g s
dz
dP = − = −
Specific weight
2.2 Pressure-Elevation Relationships (page 29)
Stevin’s Law – the pressure is the same at all points on a
horizontal plane in a particular fluid irrespective of geometry
as long as the points are connected by the same fluid.
Patm
P 1
P 2
P 3
Mercury
Water
Pressure is greater in mercury (does not equal P 3 )
2.2 Pressure-Elevation Relationships (page 29)
2.2.1 Constant Density
Pressure can be measured in terms of fluid height.
Invention of the mercury barometer is credited to
Torricelli (1608–1647).
1 mmHg = 1 Torr = 1/760 atm
http://ap-physics.david-s.org/simple-mercury-barometer/
- 760 m 760 mmHg
kg
N
m
kg 13595
Pa
N m 101325 Pa
3
2
2 1
−
h
P g h
P P g h
atm^
2.2 Pressure-Elevation Relationships (page 31)
Example 2.1: What pressure would a
diver experience at a depth of 200 ft?
The water may be considered
incompressible with a density of
62.4 lbm/ft
3
. Work entirely in fps units.
2 1 (^2 1 ) (2.10)
c c
g g P P z z h g g
− = − − =
2 1 c
g P P h g
= +
( )
2 m (^2 ) m 2 f
ft
lb (^) s 14.7 psi 62.4 200 ft ft ft lb
lb s
P
= + ^ (^)
2 f (^2 2 )
lb ft 14.7 psi 12480 ft 144 in
P
^ = + (^)
P 2 (^) = 14.7 psi +86.7 psi P 2 (^) =101.4 psia (absolute)
sea level
increasing elevation
2.2.2 Isothermal, Perfect Gas (Ideal Gas)
For gases at low pressure, the density
changes according to the ideal gas law:
Plugging this into Equation (2.9) and integrating:
R T
PM
u
2.2 Pressure-Elevation Relationships (page 31)
(2.12)
( 2 1 )
1
2 ln z z RT
gM
P
P
u
2
1
2
1
P
P
z
u z
dz RT
gM
P
dP
R T
gM z P P
u
2 1 exp (2.13)
g dz
dP
Note: Density is not
constant because it depends
on pressure.
2.2 Pressure-Elevation Relationships (page 32 )
2.2.3 Isentropic, Perfect Gas (Ideal Gas)
For a perfect gas undergoing an isentropic
process, the pressure-density relationship is:
Note that: and
Therefore:
k k Pv P
− = constant =
k
s
s
P
P
1
0 0 0
= =
=
3
3
m
kg
1
kg
m
v v
p
c
c k =
0 0 =^ =constant
− k − k P P
k
P
P
1
0
(^0)
= (2.14)
Need an
expression for ρ
as a function of P.
2.3 Manometers (page 38)
Manometer – device that uses a column of liquid to
measure pressure.
h
Patm
Pressure
Vessel
( ) 2 1 2 1
P − P = P = − g z − z
h
P 2 , z 2
P 1 , z 2
1
P gh gx gx P atm
- + − =
- Start at a point where you
know the pressure (in this
case, Patm ).
- Work your way to the other
pressure by ± ρgh.
- Decrease in elevation: +
- Increase in elevation: –
2.3 Manometers (page 39)
P 1 = Patm + gh
atm (^ m )^ o
atm m o
P P gh gh
P P gh gh gh
= + − −
= + − −
3
3
P P ( ) gh
P P gh gh gh gh
m
o m o
= + −
= + + − −
5 4
5 4
atm (^ m ) o
atm m o
P P gh gh
P P gh gh gh
= + − −
= + − −
6
6
P 2 = Patm + gh
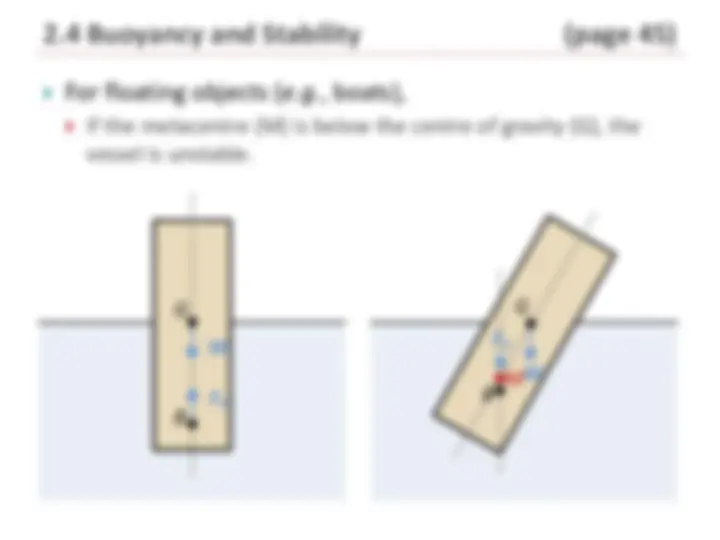
2.4 Buoyancy and Stability (page 41 )
Archimedes Principle:
An immersed object in a fluid experiences a vertical buoyant
force equal to the weight of fluid is displaces.
For an object to remain at rest within the fluid (neutrally
buoyant), the weight ( W ) must be balanced by the
buoyant force:
f displaced
W = gV
Fabove
Fbelow
Fabove = Weight from fluid above
Fbelow Fbelow = Weight from fluid above
Fabove
Fabove
Fbelow
Fabove = Weight from fluid above
Fbelow Fbelow = Weight from fluid above
Fabove
2.4 Buoyancy and Stability (page 41)
Archimedes Principle:
A floating object displaces its own weight in fluid in which it is
floating.
For an object to remain at rest at the surface, the weight
of an object ( W ) must be balanced by the buoyant force:
Only weight of liquid
is considered
because ρ liquid >> ρ gas
f displaced
W = gV