Download Set Operations and Functions: Lecture Notes and more Slides Discrete Mathematics in PDF only on Docsity!

Lecture 3

Set Operations & Set Functions

Recap

• Set: unordered collection of objects

• Equal sets have the same elements

• Subset: elements in A are also in B

• Power-set: set of all subsets

• Cartesian Product: set of ordered pairs.

1.7 Set Operations

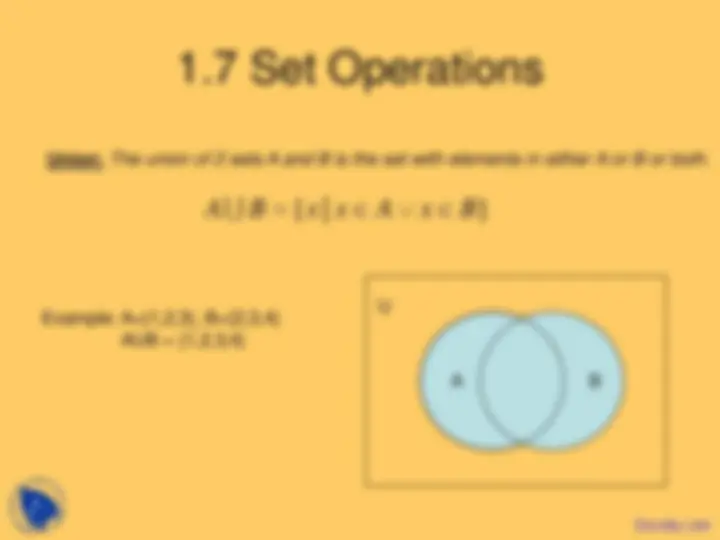
Intersection: The intersection of 2 sets A and B is the set containing elements in both A and B.

Example:

Example: A={1,2,3}, B={2,3,4} A B = {2,3}

A A B

U

A  B = { x | x ∈ A ∧ x ∈ B }

1.7 Set Operations

Sets are disjoint if their intersection is the empty set. I.e. They have no elements in common.

Principle of inclusion-exclusion: | A  B | |= A | + | B | −| A  B |

this terms is needed because elements both in A and B are counted once in AUB. Example: A={1 2 3}, B = {p,q,r}. A and B are disjoint. |AUB|=|A|+|B|=

Example: A={1 2 3}, B={1 2 3}. A=B. |AUB|=3+3-3=3.

1.7 Set Operations

A

U

Complement: The complement of a set A in U is the set U-A.

A = { x | x ∉ A }

Example: U={x|x in English alphabet} A={x| x is consonant } A = {x|x is vowel}

A A B

1.7 Set Operations

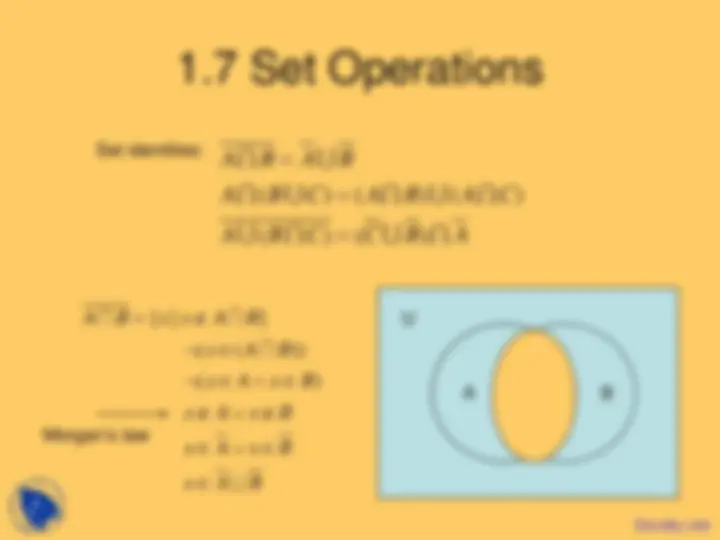
Set identities:

( ) ( ) ( )

( ) ( )

A B A B

A B C A B A C

A B C C B A

=

=

=

 

    

   

{ | } U ( ( )) ( )

A B x x A B x A B x A x B x A x B

x A x B

x A B

= ∉ ¬ ∈ ¬ ∈ ∧ ∈ ∉ ∨ ∉

∈ ∨ ∈

∈

  



Morgan’s law

1.7 Set Operations

Efficient representation in a computer: Assume arbitrary order and denote set membership with a bit string:

U={1,2,...10} (in this order) A = {1 2 3 4 5}=1 1 1 1 1 0 0 0 0 0 B = {4,5,6} = 0 0 0 1 1 1 0 0 0 0 AUB = 1 1 1 1 1 1 0 0 0 0 = BIT-wise AND = {1 2 3 4 5 6}

Example: Ai = {i,i+1,i+2....}

1

{1, 2,3,...}

n i i

A

1

{ , 1, 2,...}

n i i

A n n n

 =^ +^ +

1.8 Functions

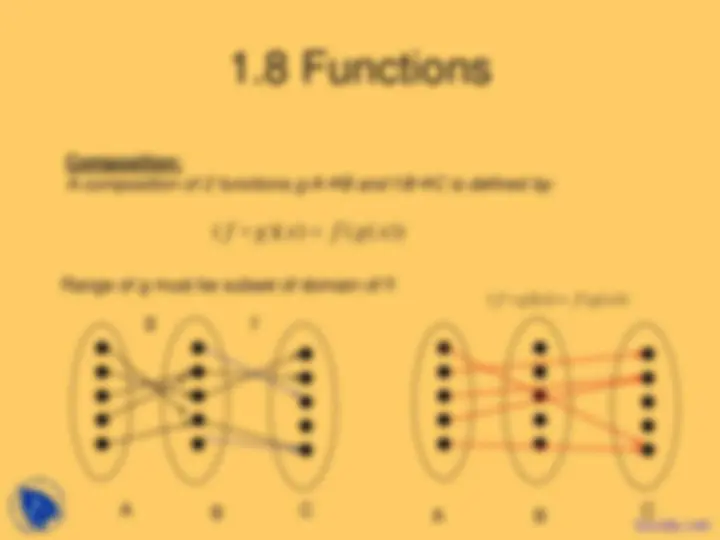
function: The assignment of exactly one element of the set B to each element

of the set A. f:A  B or f(a)=b.

A is the domain of f. B is the co-domain. of f. b is the image of a. a is the pre-image of b. range of f: set of all images of elements of A.

range

co-domain

pre- image

A

B

f

a (^) b= f(a)

domain

image

Example: f:ZZ, f(x)=x^ domain/co-domain: Z range: perfect squares {0,1,4,9,...}

1.8 Functions

One-to-one or injective function: A function f is one-to-one if and only if f(x)=f(y) implies x=y for all x,y in domain f.

A

B

it is not allowed^ f that two arrows point to the same element in B

x y f x f y x y

x y x y f x f y

( p → q ) ≡ ¬( q → ¬ p )

equivalent since:

Example: f:ZZ, f(x)=x^2 one-to-one? No; x=-1 & x=1 map both to f(1)=f(-1)=1.

1.8 Functions

( ( ) ( ))

( ( ) ( ))

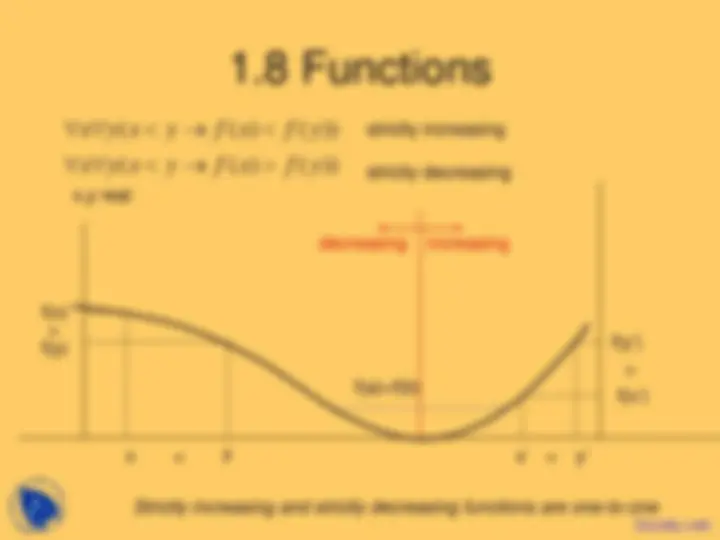
x y x y f x f y

x y x y f x f y

∀ ∀ < → <

∀ ∀ < → >

strictly increasing

strictly decreasing x,y real

x < y

f(x)

f(y)

x’ < y’

f(y’)

f(x’)

decreasing increasing

Strictly increasing and strictly decreasing functions are one-to-one

f(a)=f(b)

1.8 Functions

One-to-one correspondence or bijection: A function f is in one-to-one correspondence if it is both one-to-one and onto.

A B

f

Number of elements in A and B must be the same. Every element in A is uniquely associated with exactly one element in B.

Example: f:RR, f(x)= -x bijection!

1.8 Functions

Inverse function: The inverse function of a bijection is the function that assigns to b in B the element a in A such that f(a)=b.

f −^1 : B → A , f −^1 ( ) b = a

A B

inverse of f

A B

f

If a function is not a bijection it is not invertible: example: f:rR, f(x)=x^2.

1.8 Functions

Graph of a function: The graph of a function f is the set of ordered pairs {(a,b)|a in A, f(a)=b}.

This is a subset of the Cartesian product AXB (i.e. it is a “relation”).

a in A (for some ordering)

f(a)

Docsity.com

1.8 Functions

largest integer smaller or equal to x :Floor

smallest integer larger or equal to x: Ceiling.

! 1 2 3 ... : Factorial.

... (n times): Exponential.

log ( ) inverse of exponential (

n

b

x

x

n n

b b b b b

x x

  ^ =

Some examples:

(more details later)