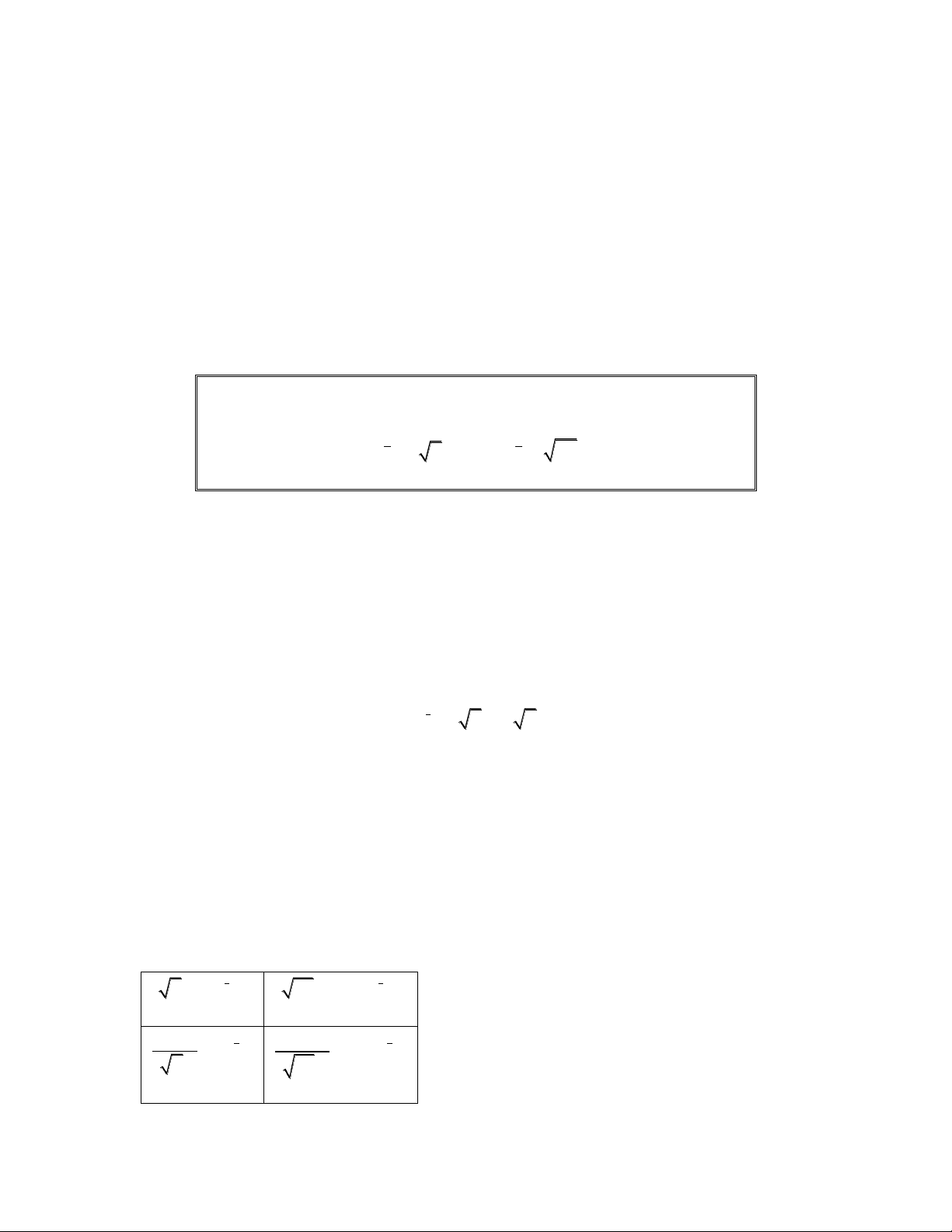








Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
We will use rational exponents to multiply or divide radical expressions having different indices. We will convert each radical expression to its equivalent ...
Typology: Exams
1 / 10

This page cannot be seen from the preview
Don't miss anything!
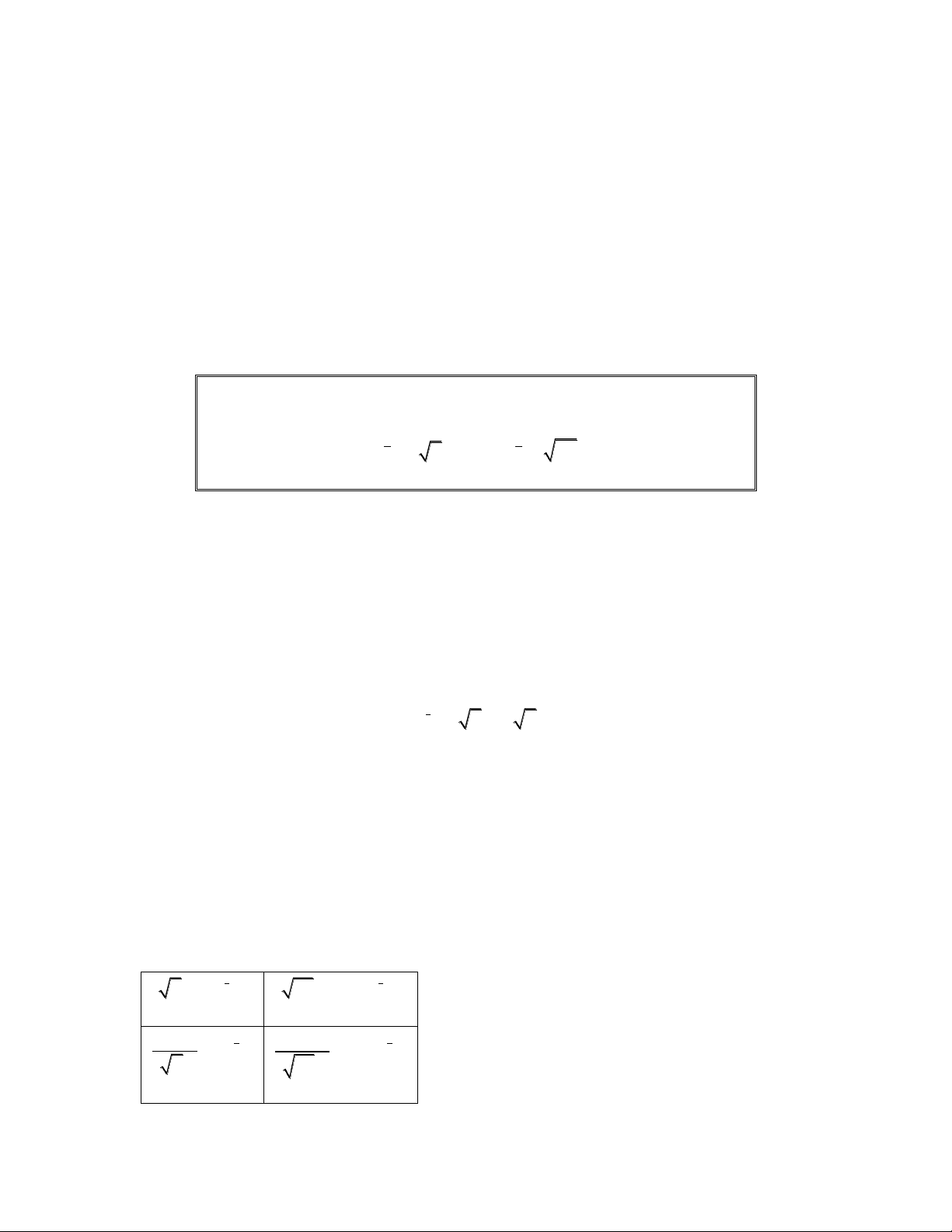






We define rational exponents as follows:
a mn^ ( na ) m and
mn n m a a
The denominator of a rational exponent is the same as the index of our radical while the numerator serves as an exponent.
Either form of the definition can be used but we typically use the first form as it will involve smaller numbers.
the definition: 1 a n^ ( n^ a )^1 na
We can use this definition to change any radical expression into an exponential expression.
Example 1. Rewrite with rational exponents.
( 5 x )^3 x^35 ( 6 3 ) x^5 (3 ) x^56
(^37) 7 3
a a
3 2
xy xy
Index is denominator , exponent is numerator
Negative exponents from reciprocals
We can also change any rational exponent into a radical expression by using the denominator as the index.
Example 2. Rewrite using radical notation.
a^53 ( 3 a )^5 (2 mn ) 27 ( 72 mn )^2
(^45) 5 4
x x
9 2
xy xy
Exponent is numerator; index is denominator
Negative exponent means reciprocals
The ability to change between exponential expressions and radical expressions allows us to evaluate expressions we had no means of evaluating previously.
Example 3. Use radical notation to rewrite and evaluate.
1632 Change to radical format; numerator is exponent , denominator is index
( 16)^3 Evaluate radical
(4)^3 Evaluate exponent
(^64) Our Answer
Example 4. Use radical notation to rewrite and evaluate.
27 ^43 Negative exponent is reciprocal
(^43)
^ Change to radical format; numerator is exponent , denominator is index
3 4
1 ( 27) Evaluate radical
4
(3) Evaluate exponent
Our Answer
Example 7. Simplify.
(^23) (^72)
2 0
x y
(^42 ) ^ x yx y (^72 0) Subtract exponents on x in denominator , y^0 1
x^ ^32 y^23 Negative exponent moves down to denominator (^23) (^32)
y x
Our Answer
We will use rational exponents to multiply or divide radical expressions having different indices. We will convert each radical expression to its equivalent exponential expression. Then, we will apply the appropriate exponent property. For our answer, we will convert the exponential expression to its equivalent radical expression. Our answer will then be written as a single radical expression.
Example 8. Multiply, writing the expression using a single radical.
(^5) x x Rewrite radical expressions using rational exponents
x^15 x^12 Need common denominator of 10 to add exponents
x^10^2 x^105 Add exponents
x^107 Rewrite as a radical expression
^10 x^7 Our Answer
Example 9. Divide, writing the expression using a single radical.
2 2
3 5
y y^ Rewrite radical expressions using rational exponents
(^23) (^25)
y y
Need common denominator of 15 to subtract exponents
(^1015) ^ yy 156 Subtract exponents
y^154 Rewrite as a radical expression
^15 y^4 Our Answer
It is important to remember that as we simplify with rational exponents, we are using the exact same properties we used when simplifying integer exponents. The only difference is we need to follow our rules for fractions as well. It may be worth reviewing your notes on exponent properties to be sure you are comfortable with using the properties.
Practice Exercises: Section 3.6 (continued)
Simplify. Your answer should contain only positive exponents.
(^34 ) 3 1
a b b b
(^53) (^54 )
2 x^2 y x y xy
(^54) (^113)
y y y
(^)
(^13 ) (^12 )
ab b a b
(^32) (^43)
(^74) 2 ( )^1
m n mn
28)^
12 23 (^32 )
y x y
(^12) (^34)
( m n^2 )^0 n
0 ( )
y x y
(^43 ) (^13)
1 2
( x y y ) x y
(^)
(^12 ) (^23)
0 4 2
( x y ) y x y
Perform the indicated operation, writing the expression using a single radical.
(^5) x 2 x
ANSWERS to Practice Exercises Section 3.6: Rational Exponents
( 10 r )
( 6 b )
(^32) 6 x
1 v^2
n ^74
(5 ) a^12
18)^413 v
v^2 u
The Answers to Practice Exercises are continued on the next page.