




















Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
An outline and examples of the proof by contradiction method in mathematics. The proof by contradiction is a logical argument where one assumes the negation of a statement and derives a contradiction, thereby establishing the original statement. proving statements with contradiction, proving conditional statements by contradiction, and combining techniques. Examples include proving the nonexistence of natural number solutions to certain equations and the existence of a prime number not in a finite set.
Typology: Lecture notes
1 / 33

This page cannot be seen from the preview
Don't miss anything!


























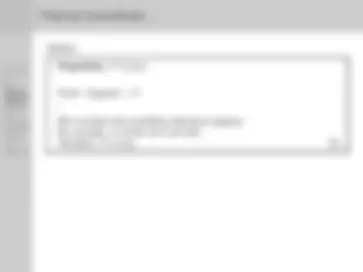
Outline:
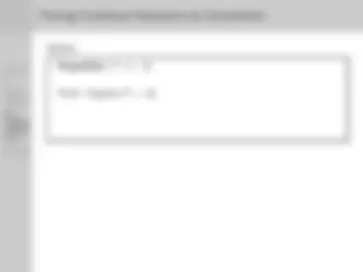
Proposition: P is true.
Proof : Suppose ∼ P.
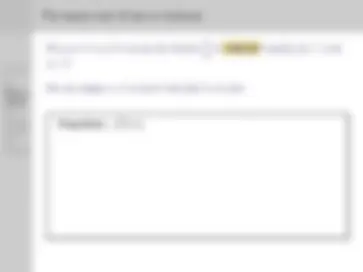
Outline:
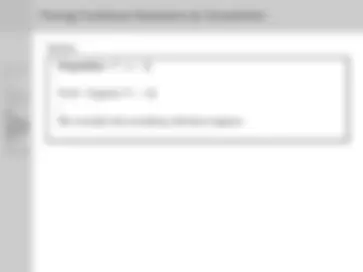
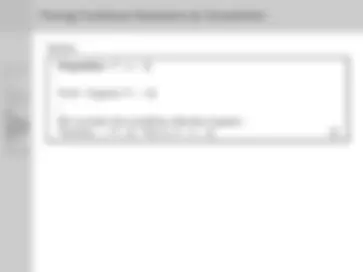
Proposition: P is true.
Proof : Suppose ∼ P. .. . We conclude that something ridiculous happens. For example, 3 is both even and odd.
Proposition: There are no natural number solutions to the equation x^2 − y 2 = 1.
Proposition: There are no natural number solutions to the equation x^2 − y 2 = 1.
Proof : Suppose x, y ∈ N and x^2 − y 2 = 1. Then (x + y )(x − y ) = 1, so x − y and x + y are divisors of 1. Then (x − y ) = (x + y ) = ±1. So, 0 = (x + y ) − (x − y ) = 2y. Therefore y = 0, contradicting that it is positive.
Proposition: There is no smallest positive rational number.
Proof : Suppose q is the smallest positive number. Then 0 < q 2 < q and q ∈ Q. This contradicts the assumption that q is the smallest positive rational number.
For p, q ∈ Z, q 6 = 0, we say the fraction
p q
is reduced if gcd(p, q) = 1 and q > 0.
For p, q ∈ Z, q 6 = 0, we say the fraction
p q
is reduced if gcd(p, q) = 1 and q > 0.
For any integer a, a^2 is even if and only if a is even.
Proposition:
For p, q ∈ Z, q 6 = 0, we say the fraction
p q
is reduced if gcd(p, q) = 1 and q > 0.
For any integer a, a^2 is even if and only if a is even.
Proposition:
Proof : Suppose
Outline:
Proposition: P =⇒ Q
Proof : Suppose P∧ ∼ Q.
Outline:
Proposition: P =⇒ Q
Proof : Suppose P∧ ∼ Q. .. . We conclude that something ridiculous happens.
Outline:
Proposition: P =⇒ Q
Proof : Suppose P∧ ∼ Q. .. . We conclude that something ridiculous happens. Therefore, ∼ P ∨ Q. That is, P =⇒ Q.
Lemma: Given integers a and b, with a > 1, if a|b then a 6 | (b + 1).
Outline:
Proposition: P =⇒ Q
Proof : Suppose P∧ ∼ Q. .. . We conclude that something ridiculous happens. Therefore, ∼ P ∨ Q. That is, P =⇒ Q.
Lemma: Given integers a and b, with a > 1, if a|b then a 6 | (b + 1).
Proof : Suppose a|b and a|(b + 1). Then there exist integers x and y such that ax = b and ay = b + 1. Then y = b+1 a = ax a+1 = x + (^1) a. Since a > 1, (^1) a is not an integer, so y is not an integer. This contradicts the assumption that y is an integer.
Lemma: Given integers a and b, with a > 1, if a|b then a 6 | (b + 1).
Theorem: Given any finite set P whose elements are prime numbers, there exists a prime number that is not in P.
Proof : Let P be a finite set whose elements are prime numbers. If P = ∅, then 3 is a prime not in P, so suppose P = {p 1 , · · · , pn} and n ≥ 1. Let n := p 1 ·... · pn + 1. Since n > 1, it has at least one prime factor p that is greater than one. By the Lemma, no element of P divides n, so p 6 ∈ P.
Lemma: Given integers a and b, with a > 1, if a|b then a 6 | (b + 1).
Theorem: Given any finite set P whose elements are prime numbers, there exists a prime number that is not in P.
Proof : Let P be a finite set whose elements are prime numbers. If P = ∅, then 3 is a prime not in P, so suppose P = {p 1 , · · · , pn} and n ≥ 1. Let n := p 1 ·... · pn + 1. Since n > 1, it has at least one prime factor p that is greater than one. By the Lemma, no element of P divides n, so p 6 ∈ P.
Example: P = { 2 , 3 , 5 , 7 , 11 , 13 }; p = 30031 = 59 × 509; 59 and 509 are not in P.