Download Counting: Permutations and Combinations and more Slides Discrete Mathematics in PDF only on Docsity!

• Lecture
• Counting 4.3,4.

4.3 Permutations

r-permutation:

An ordered arrangement of r elements of a set of n distinct elements.

Example: S={1,2,3}:

3,2,1 is a permutation of S.

3,2 is a 2-permutation of S

Note: set is unordered, but permutation is ordered! (no curly brackets).

The number of r-permutation of n objects is:

P(n,r)=n(n-1)(n-2)...(n-r+1)=n! / (n-r)!

First object can be chosen in n ways, second in (n-1) ways etc. until n-r+1.

Use product rule to get the result.

(reminder: n! = n(n-1)(n-2)...1).

4.3 Combinations

r-combination:

An unordered selection of r elements (or subset of size r) of a set of n elements.

Example: S={1 2 3 4}.

{ 3 2 1}={1 2 3} is a r-combination.

The total number of r-combinations of a set of size n is given by the

binomial coefficient: C(n,r)=n! / r! (n-r)! 0<=r<=n

Note that this is equal to P(n,r) / r!

The reason is that P(n,r) counts the total number of ordered arrangements.

However, we are only interested in unordered “arrangements” here.

For every subset of r elements one can exactly construct r! ordered arrangements,

everyone of which is included in P(n,r), but should be considered the same in C(n,r).

We thus overcounted by a factor r!, which we need to divide out.

4.3 Combinations

Remark: the expression n! / (n-r)! r! is inefficient to compute.

However, we can rewrite as follows:

n! / (n-r)! r! = n (n-1) ... (n-r+1) / r (r-1) ... 1 if r < n-r

= n (n-1) ...(r+1) / (n-r) (n-r-1) ... 1 if r > n-r

This must always be an integer (which is not so clear from the equation).

Example:

C(4,2) = number of ways to select 2 objects among 4.

S={1 2 3 4}{1 2} {1 3}{1 4}{2 3}{2 4}{3 4}

C(4,2)=6=4 3 2 1 / 2 *2.

4.3 Combinations

2. How many bit-strings of size 10 contain 4 1’s.

We need to place 4 1’s in 10 slots: C(10,4).

3. We need to form a committee of 7 people, 3 from math and 4 from computer

science to develop a discrete math course. There are 9 math candidates and

11 CS candidates.

 Two seperate problems that need to be combined using the product rule.

C(9,3) possibilities for math AND C(11,4) possibilities for CS:

Total = C(9,3) C(11,4) = 27,720.

4.3 Counting

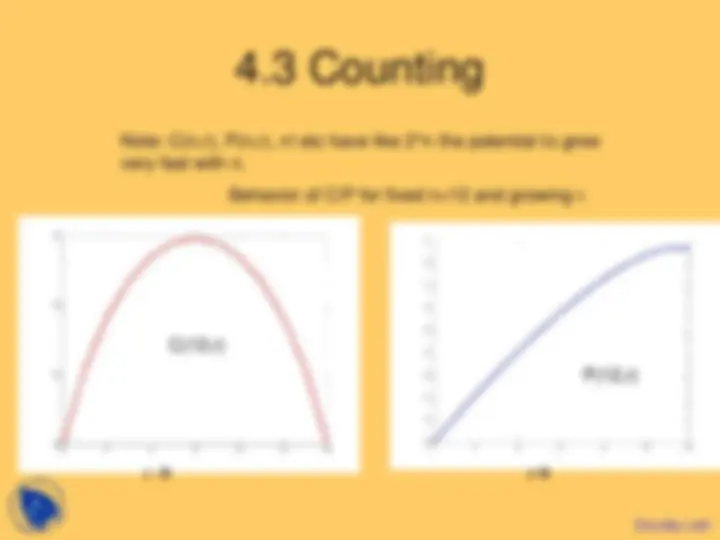
Note: C(n,r), P(n,r), n! etc have like 2^n the potential to grow

very fast with n.

C(12,r)

P(12,r)

r  r

Behavior of C/P for fixed n=12 and growing r.

4.4 Binomial Coefficients

Examples:

1. What is the coefficient of x^12 y^13 in the expansion of (x+y)^25?

I need to pick 12 x’s from 25 terms: C(25,12)=C(25,13).

2. What is the coefficient of x^12 y^13 in (2x-3y)^25?

First replace a=2x and b=-3y.

The coefficient of a^12 b^13 in (a+b)^25 is C(25,12).

thus it follows that: C(25,12) a^12 b^13 = C(25,12) 2^12 x^12 (-3)^13 y^

We already saw that the cardinality of the power-set of a set with

n elements has 2^n elements.

The total number of elements must be equal to the total number of

subsets with zeros elements (empty set) pus with 1 element, etc.

There are precisely C(n,j) ways to pick a subset of j elements from a set

with n elements, thus is follows that:

0

2

n

n

j

n

j

 

=  

 

∑

alternative proof: we know:

Now set x=1, y=1....

0

n

n n j j

j

n

x y x y

j

−

=

∑

Pascal’s identity:

1

, 0,

1

n n n

n j j n

j j j

 +     

= + ≥ ≤      

−      

Proof:

Denote T=set with n+1 elements, and S=T-{a} where a is some

arbitrary element.

The number of subsets of j elements of T is C(n+1,j).

This must be equal to the number of ways to pick j elements from T that

contain “a” plus the number of ways to pick j elements that do not contain “a”.

This number id equal to: C(n,j) (pick j elements from S) + C(n,j-1)

(pick j-1 elements from S and also pick “a”).

Hence C(n+1,j)=C(n,j)+C(n,j-1). 

This leads to Pascal’s Triangle.

From this we see an easy way to generate all coefficients

recursively.

C(4,1)+

C(4,2)=

C(5,2)

n

j r

n j

r r

Combinatorial proof using bit-strings:

Left: the number of bit-strings of length n=1 with r+1 one’s.

This must be equal to the following:

Start with all one’s s.t. last 1 is at position r+1. There is one way to do that.

Now all bitstrings s.t. last 1 is at r+2. There are C(r+1,r) ways to do that.

Generally: bitstrings s.t. last 1 is at r+k+1. There are C(r+k,r) ways to do that.

Repeat until r+k = n+1 : C(n,r) ways to do that.

Finally, all these possibilities are different, so we must add them to

get the final answer. 

4.4 Exercise 33 p. 334

one possible path.

(m,n)

How many paths are there from (0,0) to (m,n) with right and up moves as the only

allowed moves?

We need exactly, m up moves and n right moves to end in (m,n).

Let “up” be a “1” and right be a “0”. Thus we need to count the total number

of bit-strings with exactly m 1’s and n 0’s. This is equal to C(m+n,n).