








Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
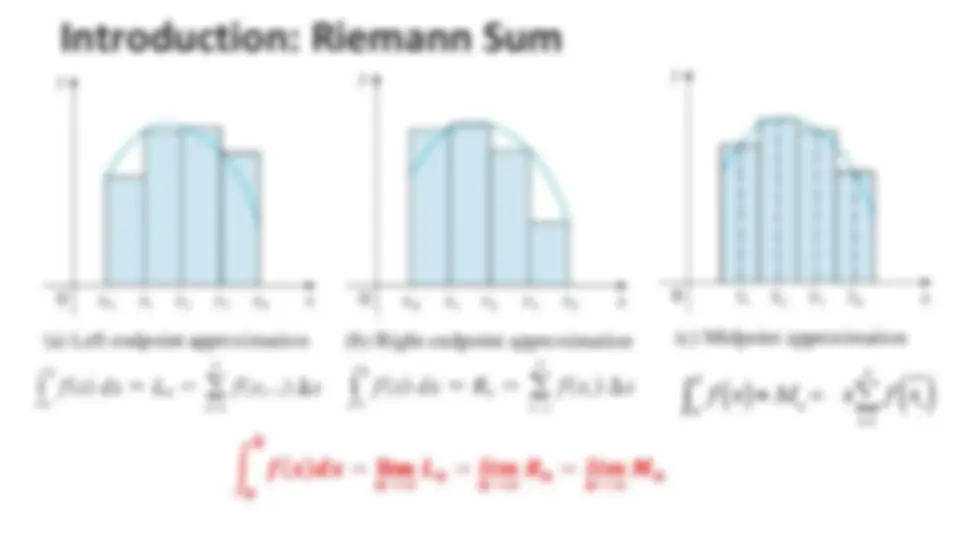
The need for numerical techniques of integration, derives the multiple-segment trapezoidal rule of integration, and uses the multiple-segment trapezoidal rule of integration to solve related applications of definite integrals. It also provides examples of how to approximate integrals using Riemann Sum and Trapezoidal Rule. formulas and calculations to illustrate the concepts.
Typology: Lecture notes
1 / 13

This page cannot be seen from the preview
Don't miss anything!








CE50P- 2
Lesson Objectives:
At the end of this lesson, students should be able to:
1.Explain the need for numerical techniques of integration,
2.derive the multiple-segment trapezoidal rule of
integration, and
3.use the multiple-segment trapezoidal rule of integration to
solve related applications of definite integrals.
Trapezoidal Rule
f ( x 0 )
f ( x 1 ) f ( x 2 )
f ( x 3 )
f ( x 4 )
a b
𝒘𝒊𝒅𝒕𝒉 =
𝒃 − 𝒂
𝒏
= 𝚫𝒙
𝚫𝒙
+
_________________________
𝑨𝟏 =
𝒃 − 𝒂
𝒏
𝒇 𝒙𝟎 + 𝒇 𝒙𝟏
𝟐
𝑨𝟐 =
𝒃 − 𝒂
𝒏
𝒇 𝒙𝟏 + 𝒇 𝒙𝟐
𝟐
𝑨𝟑 =
𝒃 − 𝒂
𝒏
𝒇 𝒙𝟐 + 𝒇 𝒙𝟑
𝟐
𝑨𝟒 =
𝒃 − 𝒂
𝒏
𝒇 𝒙𝟑 + 𝒇 𝒙𝟒
𝟐
𝑨𝑻 =
𝒃 − 𝒂
𝟐𝒏
𝒇 𝒙𝟎 + 𝟐𝒇 𝒙𝟏 + 𝟐𝒇 𝒙𝟐 + 𝟐𝒇 𝒙𝟑 + 𝒇 𝒙𝟒
Example 2
−
−
=
30
8
9 8
140000 2100
140000 2000_. t dt_
t
x ln
a) Use single segment Trapezoidal rule to find the distance covered.
b) Find the true error, for part (a).
c) Find the absolute relative true error, for part (a).
Et
a
Solution
−
−
=
30
8
9 8
140000 2100
140000 2000_. t dt_
t
x ln =^11061 m
Et = TrueValue − Approximate Value = 11061 − 11868 = − 807 m
100 11061
11061 11868
− t = = 7_._ 2959 %
Example 3
− = (^)
−
=
f(a) f(a ih) f(b ) n
b a I
n
i
1
1
2 2
n = 2 a = 8 b = 30
2
n
b a h
− = = 11
− = (^)
−
=
f( ) f(a ih) f( ) ( )
I i
8 2 30 2 2
30 8 2 1
1
(^) f ( 8 ) 2 f( 19 ) f( 30 ) 4
22 = + +
177 27 2 48475 90167 4
22 =. + (. ) +. = 11266 m
Solution
Table 1 gives the values
obtained using multiple
segment Trapezoidal rule for
n Value Et
1 11868 - 807 7.296 ---
2 11266 - 205 1.853 5.
3 11153 - 91.4 0.8265 1.
4 11113 - 51.5 0.4655 0.
5 11094 - 33.0 0.2981 0.
6 11084 - 22.9 0.2070 0.
7 11078 - 16.8 0.1521 0.
8 11074 - 12.9 0.1165 0.
−
−
=
30
8
98 140000 2100
140000 2000_. t dt t_
x ln
Table 1: Trapezoidal Rule Values for n=1,2,3,…,
t % a %
Exact Value=11061 m