Nested Quantifiers - Discrete Mathematics and its Applications - Lecture Slides, Slides of Discrete Mathematics

Download Nested Quantifiers - Discrete Mathematics and its Applications - Lecture Slides and more Slides Discrete Mathematics in PDF only on Docsity!

Discrete Math 6A

Recap

1. Proposition: statement that is true or false.
2. Logical operators: NOT, AND, OR, XOR, , 
3. Compound proposition: a new proposition by combining old ones using operators.
4. Logical equivalences: pq always true.
5. Predicate: property of a statement with variables (>3).
6. Quantifier: “there is” , “for all”. These turn statements

with variables into propositions.

1.4 Order of Quantifiers

Important: The order in which quantifiers occur can be very important!

i.e not always true.

Example: x,y real.

Is this proposition true?

∃ y ∀ x ( x + y = 0 ) ↔∀ x ∃ y ( x + y = 0 )

left: There is a y such that for all x (x+y=0). (F)

right: For all x there is a y such that x+y=0 (T)

Proposition is therefore False.

What do we learn? The order is important!

∃ y ∀ xP ( x , y )↔∀ x ∃ yP ( x , y )

However the following compound propositions are always true.

Left and right are equivalent.

( , ) ( , )

( , ) ( , )

x yP x y y xP x y

x yP x y y xP x y

∃ ∃ ↔∃ ∃

∀ ∀ ↔∀ ∀

1.4 Nested Quantifiers

Tip: You can think of expression with quantifiers as executing “loops” in

a computer program:

Example:

First loop over y and and for every y loop over x.

For every value of y, check if P(x,y) is true for all x.

If you found one, the proposition must be true.

∃ y ∀ xP ( x , y )

1.6 Sets

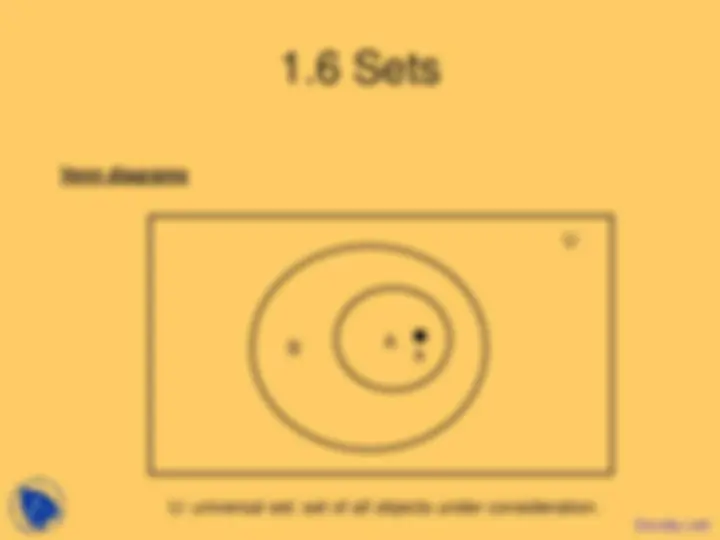
Famous sets in math: N = {0,1,2,3,...}

Z = {...,-2,-1,0,1,2,...}

Z+ = {1,2,3,...}

Q = {p/q | p in Z, q in Z, q is not 0}

R = {x | x is a real number}.

{,...} is used to indicate the the rest of the sequence once it’s clear how to

proceed {1,2,3,...}

set builder notation : {x | conditions(x) }.

This could be read as “all x such that the conditions hold true”.

Definition: Two sets are equal iff they contain the same elements.

Example: {1 2 2 3 3 3 3 4 6 } = {1 2 3 4 6} = {6 4 1 3 2}

A = B ↔ ∀ x x ( ∈ A ↔ x ∈ B )

notation for “x is an

element of B”.

1.6 Sets

Subset : A is a subset of B iff every element of A is an element of B.

A ⊆ B = ∀ x x ( ∈ A → x ∈ B )

notation for:

“A is a subset

of B”

Example: all even integers are a subset of all integers.

all Math6A students are a subset of all students.

1.6 Sets

Empty set: Set that contains no elemenst. ∅ ={}

Proposition: For any nonempty set S :

Attention:

∅ ≠ ∅{ }

( ) i ∅ ⊆ S ( ) ii S ⊆ S

Is this true?

(i) ∅ ⊆ S ↔ ∀ x x ( ∈∅ → x ∈ S )

Thus: if the right is true, the left must be true.

However, the premises: is false, and thus the implication is tue.

x ∈∅

(ii) S ⊆ S ↔ ∀ x x ( ∈ S → x ∈ S )

Clearly the right is true, so the left must be true.

1.6 Sets.

Proper Subset: A is a proper subset of B iff A is a subset of B and A is not equal to B

A ⊂ B = ( A ⊆ B ) ∧ ( A ≠ B )

Sets may contain other sets as members!

Example: {0, {a},{b}, {a,b}} = {x|x is a subset of {a,b}}

Note “a” is not “{a}”.

Cardinality: The cardinality of A is the number of distinct elements in A: |A|.

Also: S is finite in this case.

Infinite set: a set that is not finite. (e.g. all integers, real numbers).

countable uncountable

Docsity.com

1.6 sets

Cartesian product: The set of all ordered pairs (a,b) where a in A and b in B.

A × B = {( , a b ) | a ∈ A ∧ b ∈ B }

Note: we have mapped two sets to a new set.

Example: A={1,2,3} B={a,b}

AXB = {(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)}.

Note that order in (.) is important, but order in {.} is not important.

AXB is not the same as BXA! (unless A=B).

Relation: A relation between A and B is a subset of AXB.