



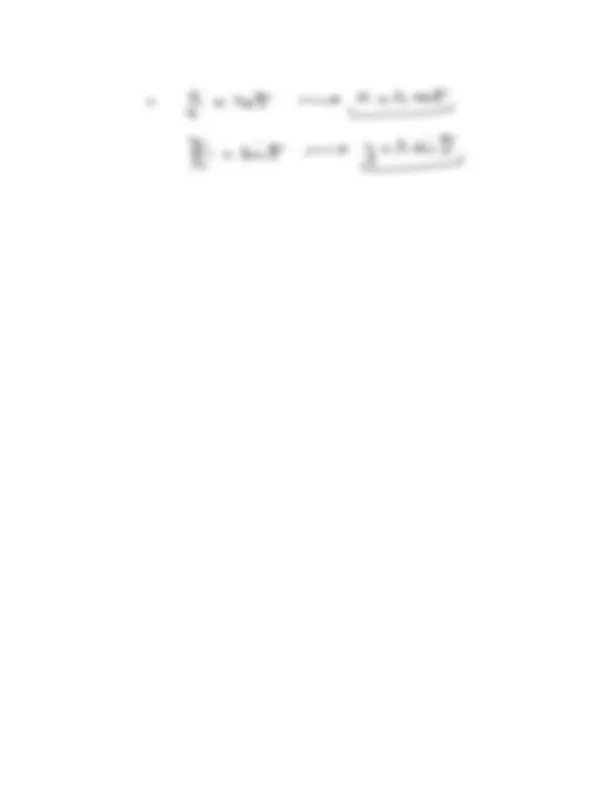


Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
This lecture explores vector-valued functions and curves in three-dimensional space (r^3). It delves into the concept of vector-valued functions, their domains, and how they define curves in space. The lecture provides examples of finding domains, describing curves, and sketching curves associated with vector-valued functions. It also includes a review of polar coordinates in two dimensions and their relationship to rectangular coordinates.
Typology: Lecture notes
1 / 8

This page cannot be seen from the preview
Don't miss anything!




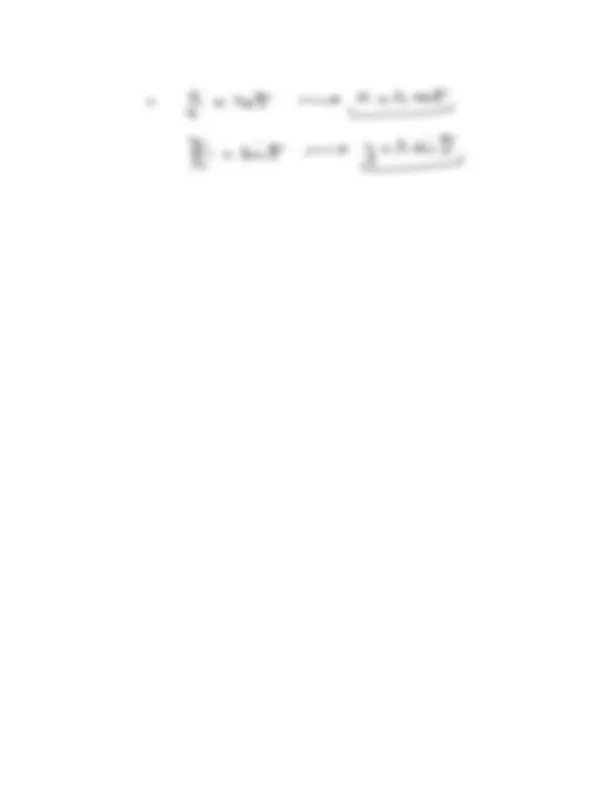
WEEK 3 LECTURE 2 Example
o D and Q 4 2 2 intersectthe^ plane a y t 2 6 Solution PG o (^) D It QC't L Ez (^) of line^ point^ PC 1 o^ D direction ve doit b to v POI^4 y z o^ Z^ D V 3 2 I a b^ c I III^ t.r.net We will^ find the spefic Value of t (^) when this line intersects^ the^ plane Xt^ y t 2 6
It 3T^ C 2E^ It^ t^6 y z 2 Zf^ G^ 2T^4 t Finally t (^2) correspond to^ the^ point on^ the^ line
1 3
7 RC (^7) 4, Y Z Z 4 (^2) It z 3 CHAPTER
RE Calculus (^) III functions f R R Now we^ will^ discuss^ functions which attack to (^) a real number^ at a vendor^ k 7 Vectorvalued
set fat^ get in componenfutations f (^) g h (^) R R
Constrains first component F^ I t i^ zo t^ z^ a a (^) second component en (^) LEED no constrains (^) here third component fft 5 t Zo^ t All (^) together we obtain that^ the domain^ ofLCE^ is 1 5 REMARII (^) Aug vector (^) valued (^) function set L fat (^) get htt
(^1123) that is traced out by the tip of^ tee moving vector ret aHitf getthe t (^) t T Equation of^ awe C fyz fqft Caparameter
Example Describe the^ curve^ determined^ by the vector valued function
L z^ t^4 3T^ Itt Solution FEI^ FEI htt curve C^ x^2 t y (^4) 3T g of^ a line C Z^ I t (^) t 2 P 2, l 1,407 4 t I (^) QU n^ o y fo p 2,4 1 y i Exemp le (^) sketch the^ curve^ associated^ to (^) thevector valued (^) function set E t't t^ E ittj t.ie Solution (^) cure C 3 x^ t yet't t any
scalar
Kmart kzo it's^ a^ distance
by
be positive (^) if movingfrom^ Ox counterclockwise negative if^ moving
ox clockwise Ex n i r R t (^) I f FI n f opc e^ n^ t I 4
PEE EI or (^) Pera If 4 REMARK ft (^) PG
4 47 Relation between^ Cx^ y
r VFL
f cost X reost 1 suit (^) y rsn