Download Kruskal’s algorithm - Advanced Data Structures and Algorithms - Solved Exam and more Exams Data Structures and Algorithms in PDF only on Docsity!
- (10 points) The diagram below shows a graph and the partition data structure from some intermediate point in the execution of Kruskal’s algorithm.
Which edges in the graph are in the partial MST solution computed so far? af, ab, bc, dg, eh, ei, eg
In the partition data structure, what is the rank ( a )? 2 What is the rank ( e )? 1
Consider an alternate version of Kruskal’s algorithm that does not use the partition data structure. Instead, when considering an edge { u , v } it does a tree traversal in the current “blue tree” containing vertex u and checks to see if v is in the tree. Give a big- O bound on the running time of this version of Kruskal’s algorithm and explain why the running time can be as bad as your bound. The bound in this case is O(mn) because we do a tree traversal for each edge and each traversal is bounded by the number of vertices in the trees traversed. While some of these trees will be small, in the worst case many of them will be large. For example, consider a graph on vertices u1,...,un where ui and ui+1 are joined by an edge of weight 1 and all other pairs of vertices are joined by edges of weight 2. In this case, the MST is a path and the “long” edges will be considered only after the entire path has been formed most of the long edges join vertices that are far apart in the path, ensuring that the tree traversal will need to visit a large fraction of the vertices.
f
a
c
b
d
e
g
h
i
f
a
c
b
d
g e
h i
CS 542 – Advanced Data Structures and Algorithms
Exam 2 Solutions
Jonathan Turner 4/1/
- (12 points) In the final analysis of the partition data structure, suppose that x is a non- singular node on level 2 and that rank ( p ( x ))=11. What is the largest value that rank ( x ) can have? Explain. rank(x) must be in a different level 1 block than rank(p(x)). That means, it must be less than 8, so its largest possible value is 7.
Now suppose that a find operation is executed and that x is one of the vertices on the “find path”. Give a lower bound on the value of rank ( p ( x )) after the find operation completes (your lower bound should be as large as possible and still be valid). Explain your answer.
rank(p(x)) must be at least 16 because a find operation at a non-singular node on level 2 causes the rank of its parent to move to a different level 1 block, and the next level 1 block following the one that contains the initial value of p(x) starts at 16.
However, we can do better in this case. Since x is non-singular, it must have a level 2 ancestor y. Rank(y)≥rank(p(x))=11 and rank(p(y)) must be in the same level 2 block as rank(y) but in a different level(1) block. If rank(y) were <16, it could not have a parent that was in the same level 2 block but a different level 1 block, since the next larger level 2 block also starts with 16. Consequently, rank(y)≥16 and rank(p(y))≥32 before the find, meaning that after the find, rank(p(x)) ≥32.
Is x still on level 2 after the find operation completes? Explain your answer. No, it is not. Before the find operation, rank(x) and rank(p(x)) were both in block(2,1)=[4,5,...,15]. After the find, rank(p(x)) is no longer in block(2,1) while rank(x) still is. So, x is no longer on level 2.
- (10 points) The diagram below shows an intermediate state in the execution of the round- robin algorithm. The partition data structure P is just shown as a collection of subsets. The leftist heaps are shown as sets of edges. The tree edges are not shown explicitly.
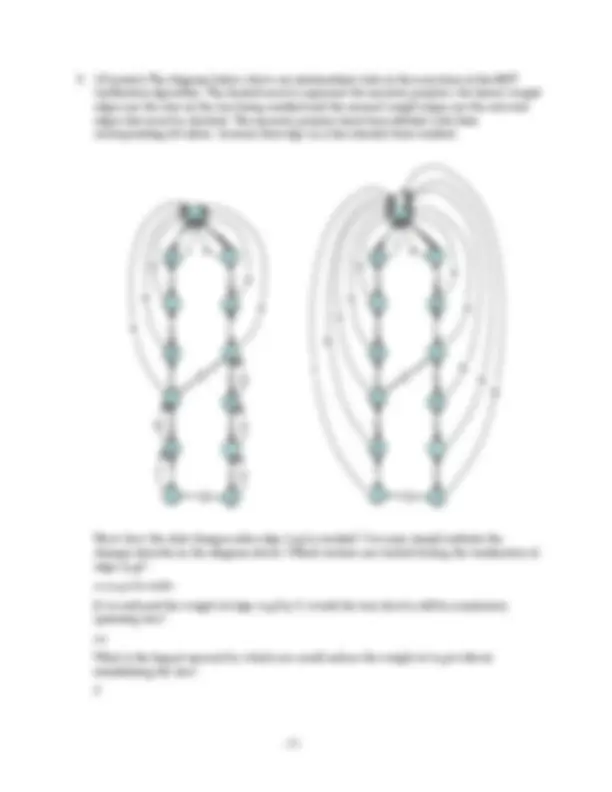
Which edges are in the partial MST that has been found so far? af, bc, eh, ej, dg, gi, gk, im
In the heap h ( d ), which edges would be considered “deleted” by the round-robin algorithm? edges dg, dk, gk, gi, im, km
Suppose that h ( d ) is the first item on the list used by the round-robin algorithm. What is the next edge added to the tree? eg
P : { a , f } { b , c } { e , h , j } { d , g , i , k , m }
h ( a ) = { af,fc,ab,ad }
h ( c ) = { cf,bc,ch,ab,bd,be }
h ( e ) = { eh,ej,be,eg,ej,ch,jh,ij }
h ( d ) = { ad,bd,dg,dk,eg,gi,gk,ij,im,km }
f
a
c
b
d
e
g
h
i
j
m
k
2 5
- (10 points) State the credit invariant used in the analysis Fibonacci heaps.
The number of credits on hand is equal to the number of distinct trees in the collection of heaps, plus two times the number of marked, non-root nodes.
Consider the node x and its children y 1 ,..., y 5 in the portion of the Fibonacci heap shown below.
Assume that x has never lost any children and that y 1 was the first to become a child of x , followed by y 2 , y 3 and so forth. Which children of x must have a mark bit that is set? Explain your answer. y 3 and y 5 must both have a mark bit that is set. When each yi became a child of x, it had to have had i– 1 children. Nodes y 2 and y 4 still have all of their children, but y 3 and y 5 both have one fewer than the number they must have had when they became children of x. Therefore, their mark bits must be set.
y 3
x
y 1 y 2 y 3 y 4 y 5
x
y 1 y 2 y 3 y 4 y 5
x
y 1 y 2 y 4 y 5
- (8 points) Suppose you are given a unit network and that you run both the “original” version of Dinic’s algorithm and the version that uses dynamic trees. Which do you expect would run faster? Explain your answer. The original will run faster. The whole point of the dynamic trees data structure is to keep track of path segments along which we can still add flow. However, in unit networks all edges have capacity 1. This means that all edges in an augmenting path get saturated, so there generally are no “left- over” path segments that can be usefully maintained in the dynamic trees data structure. As a result, we get all the overhead of maintaining the dynamic trees, but no real benefit. As a result, the version that uses dynamic trees will be slower than the original version.
