Download Understanding Linear Functions: Forms, Intercepts, and Slopes and more Slides Linear Algebra in PDF only on Docsity!
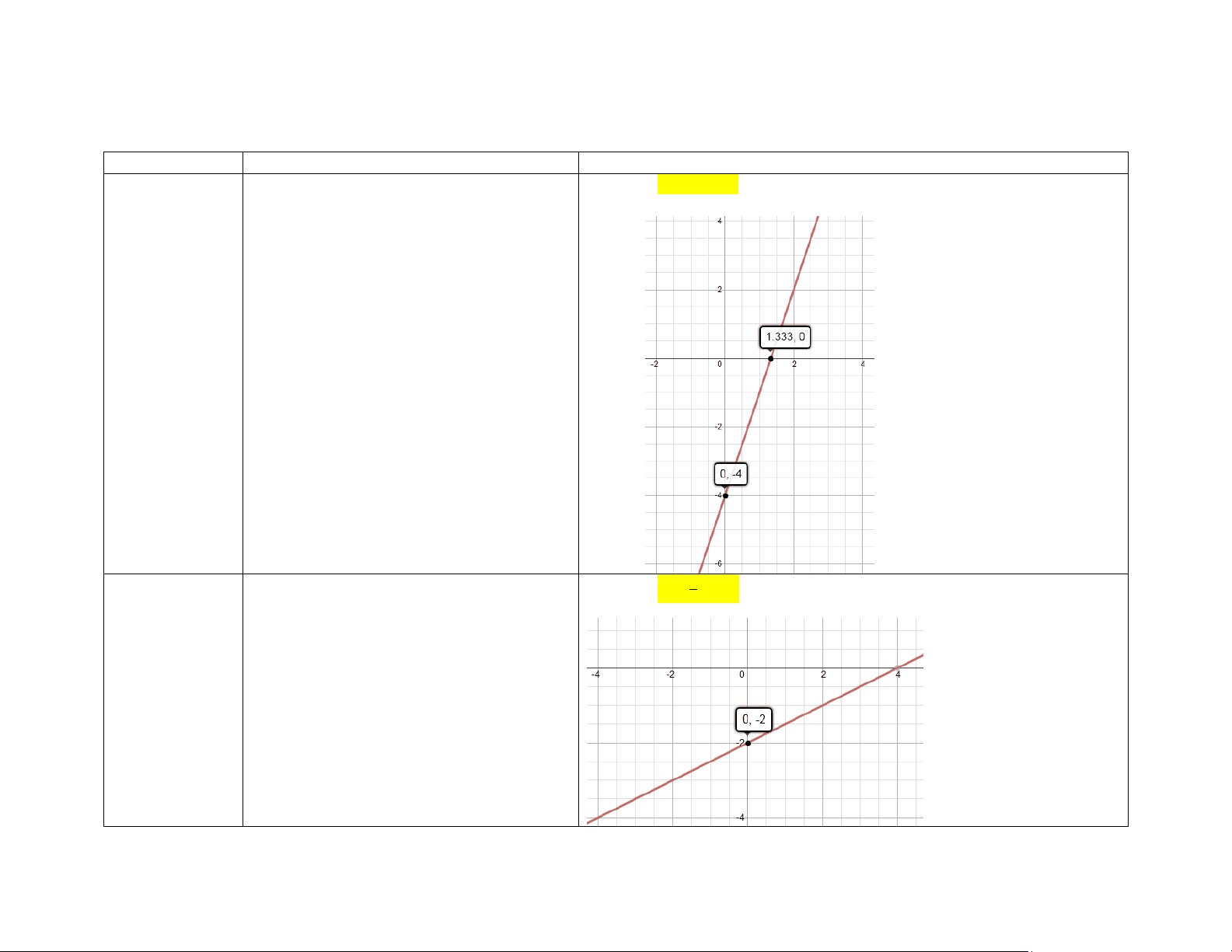
Key Terms: Forms of Linear Functions Term Definition Example and Illustration Linear function A linear function is a function whose graph is a straight line. You can usually identify the equation of a linear function by the fact that it will not have any exponents or square root symbols, and there will not be any fractions with x in the denominator. Linear functions will almost always be in one of the three forms described below (standard, slope-intercept, or point-slope). Equation: Graph: y-intercept The y-intercept is the point where the graph intercepts (crosses through) the y-axis. The x-coordinate of every y-intercept is always 0 (since any point on the y-axis has an x-coordinate of 0), which means that you can calculate the y-intercept by substituting 0 for x in the equation of the original function. In slope-intercept form, the y-intercept is also quite easy to find from the equation. Equation: The y-intercept of this function is the point .
x-intercept The x-intercept is the point where the graph intercepts (crosses through) the x-axis. The y-coordinate of every x-intercept is always 0 (since any point on the x-axis has a y-coordinate of 0), which means that you can calculate the x-intercept by substituting 0 for x in the equation of the original function. Equation: The x-intercept of this function is the point Slope The slope of a linear function is a number that represents the “steepness” of the line. The slope of a line can be positive, negative, or zero. Positive slopes move UP as the line goes to the right; negative slopes move DOWN as the line goes to the right; a slope with a value of zero is flat. The slope of a line can be thought of as the “rise over run” (how many units UP or DOWN the function moves, over how many units to the RIGHT). Positive slope: Negative slope: Zero slope:
Point-slope form of a linear function NOTE: You do not need to know how to graph or calculate with this form for this playlist, but it’s good to know what it looks like! The general form of point-slope form is usually written as , where and are real numbers. Once again, m represents the slope. Also, the point is any point on the line. This can make it useful when you’re asked to write a function with a given slope, passing through a given point – you can just plug in the requested numbers and write the point- slope form! Let’s say they ask me to write a function with a slope of - 3, passing through the point (9, - 1). That means that and I can write the point-slope form of this linear function this way: And then simplify: Here’s the graph of that function. Notice that it fulfills both conditions that were stated above:
