




Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Key concepts in linear programming, focusing on feasibility and optimality. It delves into the relationship between primal and dual problems, demonstrating how to determine if a solution is feasible and optimal. The document also provides examples and explanations of how to solve linear programming problems using the simplex method.
Typology: Exercises
1 / 7

This page cannot be seen from the preview
Don't miss anything!



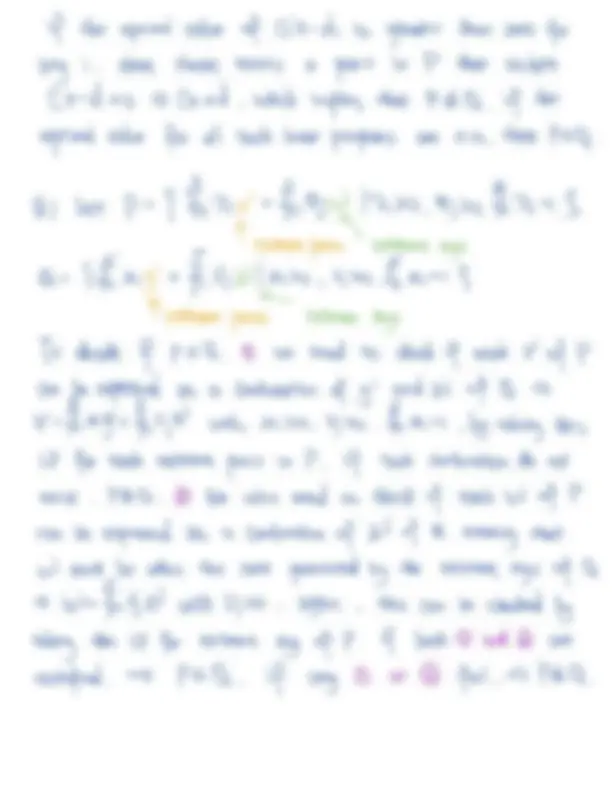
if xep^ then (^) Ax b X 0 there^ exist some PERM P'As (^0) p'b 0 PAX (^) P'b 0 Since we^ know
Xj need (^) to (^) be
PA Xj^ 0
xj oforallxep.to^ make (^) sure (^) that Ax b still valid^ according^ to Farka'slemma^ there^ exists^ avec^ to psueh that P'A (^0) P'b 0 and^ pAIpo I means that here^ is a^ redundancy (^) in te constraints^ of P^ that
to (^) be zero C Since Xi is (^) not null variable^ from
know (^) that we can (^) not find a^ vector
pA 0 pino and (^) I P'A therefore^ for with^ (^0) P'bo
ngl we need^ to have^ pA i (^0) Let x yep where yio so (^) xj y (^70) now consider^ xt A'p.in ith component he have^ A'p i
j
j y^ i^
so he^ conclude^ that xtltpsoinj
lbI Assume^ cal is True every vector (^) x that (^) satisfies Ax and (^) xs.no (^) must hate (^) xi ⼆^0 and (^) suppose b (^) is false which (^) Meansthat there is (^) no
that P'A (^) o (^) p o^ and^ pA co
by
tt (^) satisfies Ax 0 Contradicts^ a^ Thus (^) he (^) assumption that (^) Ibl is^ False leads^ to contradiction
p such that p'A 0 psoandpA.co het x be^ any vector that Ax o^ and
(^0) according assumption P'Ax would be (^0) PAX P'AiXi^ 章 P'Aj^ Xj since PA.co x so (^) then (^) P'Aix would^ be negative.he
satisfies (^) p'P
pnblemiminoyst.IP IJ.gs (^1) here is no
can (^) satisfy this inequality According^ to^ the^ duality^ heorem^ if
if he
unbounded then the dual^ mustbe infeasible In this^ case^ the prinal is (^) feasible implies that a^ nonzero P
p
T a Let^ P^ 9xER^ IAxb了^ Q^ xER (^) ICxd了^ A^ b^ C^ d^ are
vectors (^) that (^) specify the constraints (^) on PandQ To decides if P^
need (^) to check for every^ x that satisfies Axeb^ must also^ satisfies Cxed An
Cxd (^) Cxd 0 Thus (^) we can set up an (^) optimization problem (^) that maximize^ the Cxd max Cix^ di St (^) Ax b
if
cix (^) di is (^) greater than zero for any i (^) then there exists^ a^
in (^) Ptt violate Cx d.co^ Cxed^ which^ implies that (^) P (^) Q if the optimal value for all^ such^
PEQ b Let P 9
Oi 0 喜⼊i (^1 ) extremepoint i extreme rays Q (^) 倍Migi (^) ⾔Ujz
extremepoints extreme rays To decide if PEQ we^ need (^) to check if
xiofp can (^) beexpressed^ as a combination^ of yi and (^) zi
xi 蒸
Ujz with^ Miso (^) Vj 0 ⾔^ Mit (^) bysolving (^) this ⼭ (^) for each^ extreme point
such combinationdo (^) not exist PIEQ^ We also^ need^ to^ check^ if each (^) wi
(^25) of Q^ meaning that wI^ must^ lie witin the^ cone^ generated^ by the^ extreme^ rays of Q W (^) Vjzi with (^) Ui 0 again this^ can be^ checked by solving his^ Lp (^) for extreme^
satisfied (^) PEQ if any^ or fail P4Q
38201 0 and^ siti 0 C optimal cost^ CisB181^ b 15.11.38 11 品 ssi 8 In section (^) 5.2 FIb^ is defined^ as^ the^ optimal cost of
problem where^ b^ is^ the^ right
b to^ 7b where^770 the^ primal problem
Ax b^ Do^ Ax ⼊b^0
wax (^) by wax^ ⼊ by Aig
A'y c If y^ is an (^) optimal solution^ to^ the^ duel^ then ily ⽜ would
valve for deal^ wit ⼊b By strong^ duality^ Flb^ bye^ ⼊D'y ⼊FIb