Answers Inference Practice Worksheet #2
1. a) State: We will create a 90% confidence interval for a 1-sample proportion to estimate the true population
proportion of beginning algebra student who did not pass.
Plan: Parameter: p = the true population proportion of beginning algebra student who did not pass.
Random: The problem states the algebra students were randomly selected.
Independence: population of all beginning algebra students > 10(300) Condition met for independence
Large Counts: np >10 67 >10 nq > 10 233 > 10 Sample size large enough to consider
approximately Normal.
Do:
26288.0,18378.0
300
)777)(.223(.
645.1223.
90.645.1
300
)777)(.223(.
300777.0
ˆ
223.0
ˆ*
CLzsenqp
We are 90% confident the true population proportion of beginning algebra student who did not pass is in the
interval 18.2% to 26.3% for a sample size of 300 students.
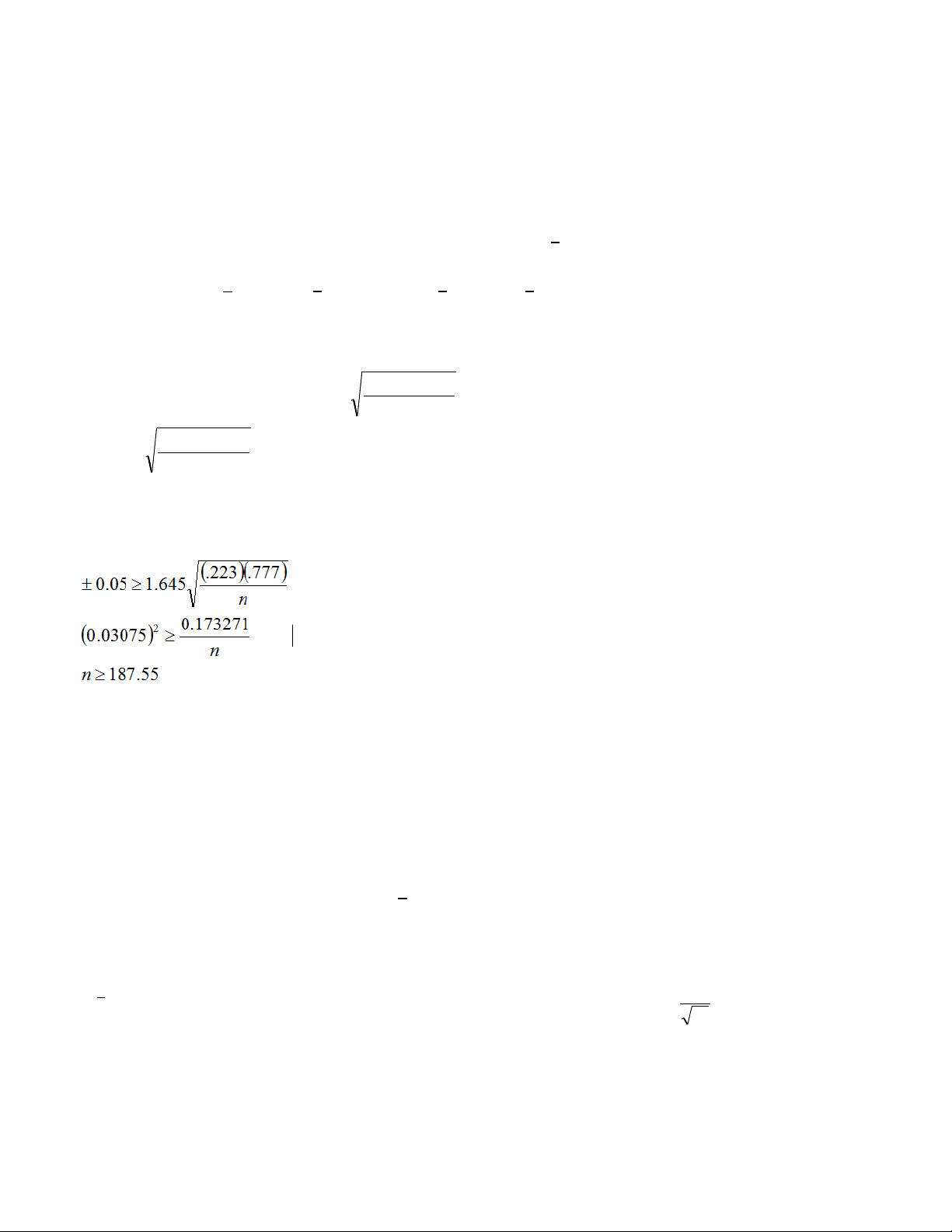
b) One would need a sample size of at least 188 beginning algebra students to
obtain a margin of error of ±5% at a 90% confidence level.
2. a) State: We will create a 95% confidence interval for a 1-sample mean to estimate the true population mean
sleep time of all people.
Plan: Parameter: µ = the true population mean sleep time of all people.
Random: The problem states a random sample of people was selected.
Independence: population of all people > 10(13) Condition met for independence
Large Counts: The problem states the distribution of average hours of sleep is Normal.
Do:
4482.8,1518.6
13
9.1
179.23.7179.295.12139.13.7 *
tCLdfnsx
We are 95% confident the true population mean sleep time of all people is in the interval 6.15 hr to 8.45 hr for a
sample of 13 people.
