Download INEQUALITIES IN TRIANGLES and more Study notes Designs and Groups in PDF only on Docsity!
I. INTRODUCTION AND FOCUS QUESTIONS
Have you ever wondered how artists utilize triangles in their artworks? Have you ever asked yourself how contractors, architects, and engineers make use of triangular features in their designs? What mathematical concepts justify all the triangular intricacies of their designs? The answers to these queries are unveiled in this module.
The concepts and skills you will learn from this lesson on the axiomatic development of triangle inequalities will improve your attention to details, shape your deductive thinking, hone your reasoning skills and polish your mathematical communication. In short, this module unleashes that mind power that you never thought you ever had before!
Remember to find out the answers to this essential question: “How can you justify inequalities in triangles?”
II. LESSONS AND COVERAGE
In this module, you will examine this question when you take the following lessons:
Lesson 1 – Inequalities in Triangles
1.1 Inequalities among Sides and among Angles of a Triangle 1.2 Theorems on Triangle Inequality 1.3 Applications of the Theorems on Triangle Inequality
INEQUALITIES IN
TRIANGLES
In these lessons, you will learn to: Lesson 1 • state and illustrate the theorems on triangle inequalities such as exterior angle inequality theorem, triangle inequality theorem, hinge theorem.
- apply theorems on triangle inequalities to: a. determine possible measures for the angles and sides of triangles. b. justify claims about the unequal relationships between side and angle measures; and
- use the theorems on triangle inequalities to prove statements involving triangle inequalities.
Module MapModule Map
Inequalities in Triangle
Inequalities in One Triangle
Inequalities in Two Triangles
Triangle Inequality Theorem 1(Ss → Aa)
Triangle Inequality Theorem 1(Aa → Ss)
Triangle Inequality Theorem 3(S 1 +S 2 >S 3 )
Exterior Angle Inequality Theorem
Hinge Theorem
Converse of Hinge Theorem
- From the inequalities in the triangles shown, a conclusion can be reached using the converse of hinge theorem. Which of the following is the last statement?
a. HM ≅ HM c. HO ≅ HE b. m ∠ OHM > m ∠ EHM d. m ∠ EHM > m ∠ OHM
- Hikers Oliver and Ruel who have uniform hiking speed walk in opposite directions- Oliver, eastward whereas Ruel, westward. After walking three kilometers each, both of them take left turns at different angles- Oliver at an angle of 30^0 and Ruel at 40^0. Both continue hiking and cover another four kilometers each before taking a rest. Which of the hikers is farther from their point of origin?
a. Ruel c. It cannot be determined. b. Oliver d. Ruel is as far as Oliver from the rendezvous.
- Which of the following is the accurate illustration of the problem?
a.
b.
c.
d.
E
H
O
M
- The chairs of a swing ride are farthest from the base of the swing tower when the swing ride is at full speed. What conclusion can you make about the angles of the swings at different speeds?
a. The angles of the swings remain constant whether the speed is low or full. b. The angles of the swings are smaller at full speed than at low speed. c. The angles of the swings are larger at full speed than at low speed. d. The angles of the swings are larger at low speed than at full speed.
- Will you be able to conclude that EM > EF if one of the following statements is not established: AE ≅ AE , AF ≅ AM , m ∠ MAE > m ∠ FAE?
a. Yes, I will. b. No, I won’t. c. It is impossible to decide. d. It depends on which statement is left out.
- Which side of ∆ GOD is the shortest?
a. GO c. DG b. DO d. GD
- The diagram is not drawn to scale. Which of the following combined inequalities describes p,q,r,s , and t?
a.
b.
c.
d.
F E^ M
A
36 o 42 o
86 o
49 o G
O
D
P
q
r
t
s
59 o
59 o
60 o 61 o
p < q < r < s < t
s < p < q < r < t
t < r < s < q < p
q < p < t < r < s
- Which of the following theorems justifies your response in item no. 15?
I. Triangle Inequality Theorem 1 II. Triangle Inequality Theorem 2 III. Triangle Inequality Theorem 3 IV. Hinge Theorem V. Converse of Hinge Theorem
a. I, II, and III b. IV only c. IV and V d. V only
- If the owner would like the same height for both houses, which of the following is true?
I. Roof costs for the larger lot is higher than that of the smaller lot. II. The roof of the smaller house is steeper than the larger house.
a. I only c. neither I nor II b. II only d. I and II
- What considerations should you emphasize in your design presentation so that the balikbayan would award you the contract to build the houses?
I. Kinds of materials to use considering the climate in the area II. Height of floor-to-ceiling corner rooms and its occupants III. Extra budget needed for top-of-the-line furnishings IV. Architectural design that matches the available funds V. Length of time it takes to finish the project
a. I, II, and IV c. I, II, IV, and V b. I, IV, and V d. I, II, III, IV, V
- Why is it not practical to design a house using A-Frame style in the Philippines?
I. A roof also serving as wall contributes to more heat in the house. II. Placement of the windows and doors requires careful thinking. III. Some rooms of the house would have unsafe low ceiling. IV. An A-Frame design is an unusually artful design.
a. I and III c. I, II, and III b. II and IV d. I, II, III, IV
- Why do you think an A-Frame House is practical in countries with four seasons?
A. The design is customary. B. An artful house is a status symbol. C. The cost of building is reasonably low. D. The snow glides easily on steep roofs.
Lesson
Inequalities in
Triangles
What to KnowWhat to Know
Let’s start the module by doing three activities that will reveal your background knowledge on triangle inequalities.
MY DECISIONS NOW AND THEN LATER
A ctivity^1
Directions:
- Replicate the table below on a piece of paper.
- Under the my-decision-now column of the first table, write A if you agree with the statement and D if you don’t.
- After tackling the whole module, you will be responding to the same statements using the second table.
Statement My Decision Now
1 To form a triangle, any lengths of the sides can be used. 2 The measure of the exterior angle of a triangle can be greater than the measure of its two remote interior angles. 3 Straws with lengths 3 inches, 4 inches and 8 inches can form a triangle. 4 Three segments can form a triangle if the length of the longest segment is greater than the difference but less than the sum of the two shorter segments. 5 If you want to find for the longest side of a triangle, look for the side opposite the largest angle.
Statement My Decision Later
1 To form a triangle, any lengths of the sides can be used. 2 The measure of the exterior angle of a triangle can be greater than the measure of its two remote interior angles. 3 Straws with lengths 3 inches, 4 inches and 8 inches can form a triangle. 4 Three segments can form a triangle if the length of the longest segment is greater than the difference but less than the sum of the two shorter segments. 5 If you want to find for the longest side of a triangle, look for the side opposite the largest angle.
Note that the triangles in this concept museum are not drawn to scale and all sides can be named using their endpoints. Consider using numbers to name the angles of these triangles.
Notice that markings are shown to show which angles are larger and which sides are longer. These markings serve as your hints and clues. Your responses to the tasks must be justified by naming all the theorems that helped you decide what to do.
How many tasks of the concept museum can you tackle now?
Replicate two (2) copies of the unfilled concept museum. Use the first one for your responses to the tasks and the second one for your justifications.
Write two Inequalities to describe angle 1.
Write a detailed if- then statement to describe triangles MXK and KBF if angle X is larger than angle B
Write a detailed if-then statement to describe triangles MXK and KBF if MK is longer than KF.
Write an if-then statement about the angles given the marked sides.
Write the combined inequality you will use to determine the length of MK?
Write if-then statement about the angles given the marked sides.
Write if-then statement about the sides given the marked angles.
Write two Inequalities to describe angle 2.
Write an if-then statement about the sides given the marked angles
5
Knowing TH>TX>HX, what question involving inequality should you use to check if they form a triangle?
Write three inequalities to describe the sides of this triangle
1 3 4
2 C
N
H^ E
X
T
M
K
F
B
W
6 7
MY
CONCEPT
MUSEUM
on TRIANGLE INEQUALITIES Come visit now!
R
5
1 3 4
2 C
N
H E
X
T
M
K
F
B
W
6 7
MY CONCEPT MUSEUM on TRIANGLE INEQUALITIES Come visit now!
R
1. Axioms of Equality 1.1 Reflexive Property of Equality - For all real numbers p , p = p. 1.2 Symmetric Property of Equality - For all real numbers p and q , if p = q , then q = p. 1.3 Transitive Property of Equality - For all real numbers p , q , and r , if p = q and q = r , then p = r. 1.4 Substitution Property of Equality - For all real numbers p and q , if p = q , then q can be substituted for p in any expression.
Are you excited to completely build your concept museum, Dear Concept Contractor? The only way to do that is by doing all the succeeding activities in the next section of this module. The next section will also help you answer this essential question raised in the activity Artistically Yours: How can you justify inequalities in triangles? The next lesson will also enable you to do the final project that is inspired by the artworks shown in Artistically Yours. When you have already learned all the concepts and skills related to inequalities in triangles, you will be required to make a model of a folding ladder and justify the triangular features of its design. Your design and its justification will be rated according to these rubrics: accuracy, creativity, efficiency, and mathematical justification.
What to ProcessWhat to Process
Your first goal in this section is to develop and verify the theorems on inequalities in triangles. To succeed, you need to perform all the activities that require investigation.
When you make mathematical generalizations from your observations, you are actually making conjectures just like what mathematicians do. Hence, consider yourself little mathematicians as you perform the activities.
Once you have developed these theorems, your third goal is to prove these theorems. You have to provide statements and/or reasons behind statements used to deductively prove the theorems.
The competence you gain in writing proofs enables you to justify inequalities in triangles and in triangular features evident in the things around us.
Before you go through the process, take a few minutes to review and master again the knowledge and skills learned in previous geometry lessons. The concepts and skills on the following topics will help you succeed in the investigatory and proof-writing activities.
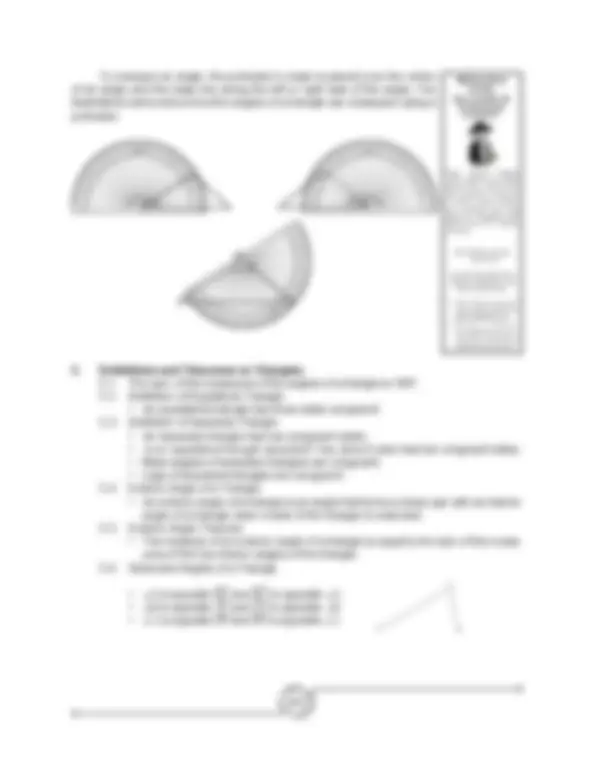
To measure an angle, the protractor’s origin is placed over the vertex of an angle and the base line along the left or right side of the angle. The illustrations below show how the angles of a triangle are measured using a protractor.
(^0180)
(^20160)
(^30150)
(^40140)
5013060120
(^7011080100 ) 6050130 40140 30150 20160 10 10170 (^17032) o 0180
1800 16020 15030 (^14040) (^13050) (^12060) (^11070) 9010080 (^16015030 )
(^1701020)
17010
1800
108 o
(^0180)
(^20160)
(^30150)
(^40140)
5013060120
(^7011080100 ) 6050130 40140 30150 20160 10 10170 (^17040) o 0180
Mathematical History Who invented the first advanced protractor?
Capt. Joseph Huddart (1741-1816) of the United States Navy invented the first advanced protractor in 1801. It was a three- arm protractor and was used for navigating and determining the location of a ship
~Brian Brown of www. ehow.com~ To read more about the history of protractor, visit these website links:
- http://www.counton. o r g / m u s e u m / f l o o r 2 / gallery5/gal3p8.html
- h t t p : / / w w w. a b l o g a b o u t h i s t o r y. com/2011/07/29/the- worlds-first-protractor/ 5. Definitions and Theorems on Triangles 5.1 The sum of the measures of the angles of a triangle is 180º. 5.2 Definition of Equilateral Triangle
- An equilateral triangle has three sides congruent. 5.3 Definition of Isosceles Triangle
- An isosceles triangle has two congruent sides.
- Is an equilateral triangle isosceles? Yes, since it also has two congruent sides.
- Base angles of isosceles triangles are congruent.
- Legs of isosceles triangles are congruent. 5.4 Exterior Angle of a Triangle
- An exterior angle of a triangle is an angle that forms a linear pair with an interior angle of a triangle when a side of the triangle is extended. 5.5 Exterior Angle Theorem
- The measure of an exterior angle of a triangle is equal to the sum of the meas- ures of the two interior angles of the triangle. 5.6 Sides and Angles of a Triangle
- ∠ S is opposite EC and EC is opposite ∠ S.
- ∠ E is opposite SC and SC is opposite ∠ E
- ∠ C is opposite ES and ES is opposite ∠ C.
Internet Learning Mastering the Triangle Congruence Postulates Video • http://www.onlinemathlearn- ing.com/geometry-congru ent-triangles.html - Interactive • http://www.mrperezonlin emathtutor.com/G/1_5_Prov ing_Congruent_SSS_SAS_-
- ASA_AAS.htmlhttp://nlvm.usu.edu/ e n / n a v / f r a m e s _ a s i d _ 1 6 5 _ g _ 1 _ t _ 3.
- html?open=instructionshttp://www.mangahigh.com/ en/maths_games/shape/ congruence/congruent_ triangles?localeset=en 6. Definition and Postulates on Triangle Congruence
6.1 Definition of Congruent Triangles: Corresponding parts of congruent triangles are congruent (CPCTC). 6.2 Included Angle
- Included angle is the angle formed by two distinct sides of a triangle.
- ∠ YES is the included angle of EY and ES
- ∠ EYS is the included angle of YE and YS
- ∠ S is the included angle of SE and SY
6.3 Included Side
- Included side is the side common to two angles of a triangle.
- AW is the included side of ∠ W A E and ∠ E W A
- EW is the included side of ∠ A E W and ∠ A W E
- AE is the included side of ∠ W A E and ∠ A E W 6.4 SSS Triangle Congruence Postulate 6.5 SAS Triangle Congruence Postulate 6.6 ASA Triangle Congruence Postulate 7. Properties of Inequality 7.1 For all real numbers p and q where p > 0, q > 0:
- If p > q , then q < p.
- If p < q , then q > p. 7.2 For all real numbers p , q, r and s , if p > q and r ≥ s , then p + r > q + s. 7.3 For all real numbers p , q and r , if p > q and r > 0, then pr > qr. 7.4 For all real numbers p , q and r , if p > q and q > r , then p > r. 7.5 For all real numbers p , q and r , if p = q + r , and r > 0, then p > q.
The last property of inequality is used in geometry such as follows:
P Q R
P
Q R
Q is between P and R.
PR ≅ PQ + QR Then PR > PQ and PR > QR.
∠ 1 and ∠ 2 are adjacent angles.
∠ PQR ≅ ∠1 + ∠ 2
Then m ∠ PQR > m ∠1 and m ∠ PQR > m ∠ 2
E
Y
S
A
W
E
The following steps have to be observed in writing proofs:
- Draw the figure described in the problem. The figure may have already been drawn for you, or you may have to draw it yourself.
- Label your drawn figure with the information from the given by:
marking congruent or unequal angles or sides, marking perpendicular, parallel or intersecting lines or indicating measures of angles and/or sides
The markings and the measures guide you on how to proceed with the proof they also direct you whether your plan for proof requires you to make additional constructions in the figure.
- Write down the steps carefully. Some of the first steps are often the given statements (but not always), and the last step is the statement that you set out to prove. 11. How to Write an Indirect Proof 11.1 Assume that the statement to be proven is not true by negating it. 11.2 Reason out logically until you reach a contradiction of a known fact. 11.3 Point out that your assumption must be false; thus, the statement to be proven must be true. 12. Greatest Possible Error and Tolerance Interval in Measurements You may be surprised why two people measuring the same angle or length may give different measurements. Variations in measurements happen because measurement with a measuring device, according to Donna Roberts (2012), is approximate. This variation is called uncertainty or error in measurement, but not a mistake. She added that there are ways of expressing error of measurement. Two are the following:
Greatest Possible Error (GPE) One half of the measuring unit used is the greatest possible error. For example, you measure a length to be 5.3 cm. This measurement is to the nearest tenth. Hence, the GPE should be one half of 0.1 which is equal to 0.05. This means that your measurement may have an error of 0.05 cm, that is, it could be 0.05 longer or shorter.
Tolerance Intervals Tolerance interval (margin of error) may represent error in measurement. This interval is a range of measurements that will be tolerated or accepted before they are considered flawed.
Supposing that a teacher measures a certain angle x as 36 degrees. The measurement is to the nearest degree, that is, 1. The GPE is one half of 1, that is, 0.5. Your answer should be within this range: 36-0.5 ≤ x ≤ 36 + 0.5. Therefore, the tolerance interval or margin of error is 35.5≤ x ≤36.5 or 35.5 to 36.5.
Now that you have already reviewed concepts and skills previously learned that are useful in this module, let us proceed to the main focus of this section—develop, verify, and prove the theorems on inequalities in triangles.
WHAT IF IT’S LONGER?
A ctivity^4
Materials Needed: protractor, manila paper, ruler Procedures:
- Replicate the activity table on a piece of manila paper.
- Measure using a protractor the angles opposite the sides with given lengths. Indicate the measure in your table.
- Discover the relationship that exists between the lengths of the sides of triangles and the angles opposite them. Write them on manila paper.
Triangle Length of Sides
Measures of Angles Opposite the Sides
∆ FUN
FN 3.5 (^) m ∠ U
NU 4.5 (^) m ∠ F
∆ PTY
TP (^5) m ∠ Y
PY 6 m ∠ T
∆ RYT
RY (^5) m ∠ T
TY (^10) m ∠ R
T
U
F
4.5 N
T
Y 6 P^
R 5 Y
B. The diagrams in the exercises are not drawn to scale. If each diagram were drawn to scale, list down the sides and the angles in order from the least to the greatest measure.
∆ NAY ∆ FUN ∆ WHT
Sides Angle
C. Your parents support you in your studies. One day, they find out that your topic in Grade 8 Math is on Inequalities in Triangles. To assist you, they attach a triangular dart board on the wall with lengths of the sides given.
They say they will grant you three wishes if you can hit with an arrow the corner with the smallest region and two wishes if you can hit the corner with the largest region.
- Which region should you hit so your parents will grant you three wishes?
- Which region should you hit so your parents will grant you two wishes?
Grant: 3 wishes
Grant: 2 wishes Region to Hit with an Arrow
Mathematics in Art Geometric Shapes for Foundation Piecing by Dianna Jesse
Challenge:
- Which figure is drawn first in the artworks--the smallest polygon or the largest polygon?
- Make your own design by changing the positions or the lengths of the sides of the triangles involved in constructing the figure.
- Would you like to try using the hexagon? Visit this web link to see the artworks shown: http://dian- najessie.wordpress.com/tag/ triangular-design/~
WHAT IF IT’S LARGER?
A ctivity^5
Materials Needed: ruler, manila paper Procedures:
- Replicate the activity table on a piece of Manila paper.
- Measure using ruler the sides opposite the angles with given sizes. Indicate the lengths (in mm) on your table.
- Develop the relationship of angles of a triangle and the lengths of the sides opposite them by answering the questions below on a piece of Manila paper.
Triangle Measure of the Angles Lengths of Sides Opposite the Angles
∆ LYF
m ∠ L FY m ∠ Y LF m ∠ F LY
∆ QUT
m ∠ Q TU m ∠ U QT m ∠ T QU
∆ OMG
m ∠ O MG m ∠ M GO m ∠ G MO
Q
U
E^ S^ T^ I^ O N
S
?
- Is there a relationship between the size of an angle and the length of the side opposite it? Yes, there is. No, there isn’t.
- Making Conjecture: What is the relationship between the angles of a triangle and the sides opposite them?
- When one angle of a triangle is larger than a second angle, the side opposite the _______________________________.
- Your findings in no. 2 describe Triangle Inequality Theorem 2. Write it in if-then form.
- What is the relationship between the largest angle of a triangle and the side opposite it?
- What is the relationship between the smallest angle of a triangle and the side opposite it?
36 o^38 o^61 o
81 o 48 o
103 o^29 o
L Q (^) O
T U G M Y (^) F
54 o
90 o
