Generalized Permutations - Discrete Mathematics and its Applications - Lecture Slides, Slides of Discrete Mathematics

Download Generalized Permutations - Discrete Mathematics and its Applications - Lecture Slides and more Slides Discrete Mathematics in PDF only on Docsity!

Lecture 6

Generalized Permutations and

Combinations

Recap

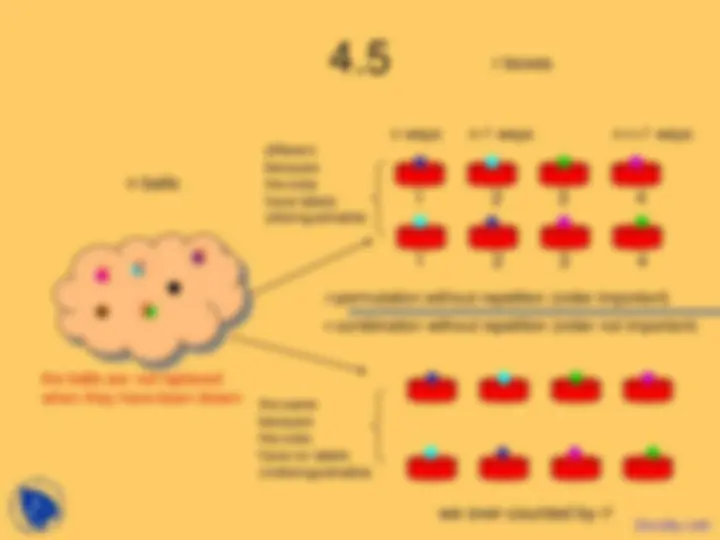
r-permutations: The number of ways in which we can draw r balls from a collection of n different balls, where the order is important: P(n,r) = n! / (n-r)! r-combinations: The number of ways in which we can draw r balls from a collection of n different balls, where we do not care about the ordering: C(n,r) = n! / r! (n-r)! Today: we study counting problems where repetitions are allowed, i.e. it is possible that the same ball is drawn multiple times.

n balls r boxes 1 2 3 4 n ways n ways n ways 1 2 3 4 r-permutation with repetition (order important) r-combination with repetition (order not important) the balls are replaced when they have been drawn. Or there is a very large stack of indistinguishable balls of each color. this one is tricky! different because the slots have labels (distinguishable) the same because the slots have no labels (indistinguishable)

Example: We want to draw 2 pieces of fruit from a bowl that contains many 2 apples, 2 pears, and 2 oranges. In how many ways can we do this such that:

1. The apples are different and the order matters.
2. The apples are different and the order does not matter.
3. The apples are indistinguishable but the order matters.
4. The apples are indistinguishable and the order does not matter.  1) 6 * 5 = 30 P(6,2)  2) 6 * 5 / 2 = 15 C(6,2)  3) Now there are 3 kinds of fruit that we draw with replacement (since there are enough of each kind to be able to pick any fruit at any draw). This is true because drawing apple 1 is no different than drawing apple 2. It’s like there are copies of the same apple present. Thus: 3 * 3 = 9 ( a a), (a p), (a o), (p a), (p p), (p o), (o a), (o p), (o o).  4) Since the order doesn’t matter (a p) = (p a), idem (a o)=(o a), (p o)=(o p). we over-counted 3 pieces: 9-3 = 6.

• r-permutation without repetition
• order matters (r distinguishable slots)
• without replacement (n distinguishable objects) n! / (n-r)! - r-combination without repetition - order does not matter (r indistinguishable slots) - without replacement (n distinguishable objects) n! / r! (n-r)!
• r-permutation with repetition
• order matters (r distinguishable slots)
• with replacement (n distinct classes of indistinguishable objects) n^r n is number of distinct classes of objects in the original bag! - r-combination with repetition - order does not matter (r indistinguishable slots) - with replacement (n distinct classes of indistinguishable objects) (n+r-1)! / r! (n-1)!

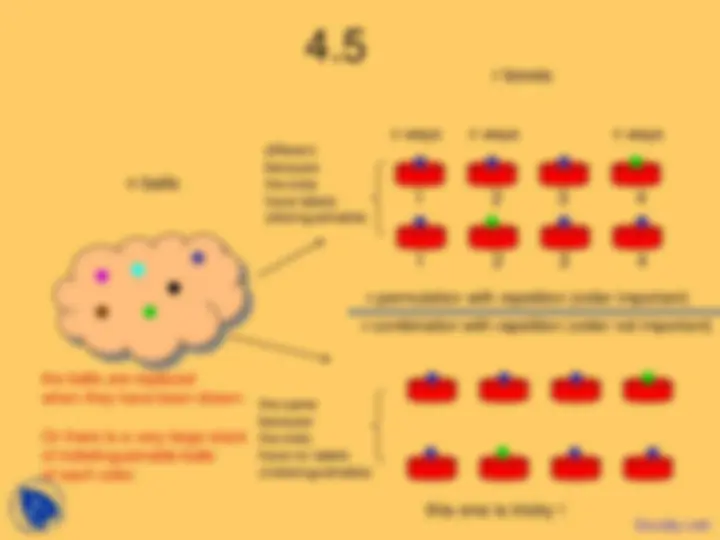
Another problem: Assume we have exactly n objects in a bag, and we are going to draw all of them. The order in which we draw them is important, however n1 objects are indistinguishable, n2 different objects are indistinguishable etc. This is like: you can only replace the blue ball 2 times, the red ball 3 times etc.) (b b r r r) is different from (b r b r b r), but the blue balls are the same and the red balls are the same. (2 distinct classes of indistinguishable balls of size 2 and 3 and distinguishable slots). Here we can first count the total number of permutations, pretending all balls are different  n! (n = number of balls, not kinds of balls) Now try to figure out which strings are equivalent: (b1 b2 r1 r2 r3) = (b2 b1 r1 r2 r3). There are 2! ways to permute the blue balls. (b1 b2 r2 r2 r3) = (b1 b2 r2 r1 r3). There are 3! ways to permute the red balls.

Docsity.com

Yet another problem: In how many ways can we distribute n different objects into k different boxes such that n1 objects go in box 1, n2 objects go in box 2,... nk objects go in box k. (k distinguishable boxes with n distinguishable balls) 4 1 (^6 ) 2 (b r r b b g) Trick: the colors are now the boxes, so we assign boxes to balls instead of balls to boxes! From the previous problem we know there are n!/n1! n2!...nk! ways to assign the boxes with k colors to the n balls.

Examples:

1. How many ways are there to select five bills from a cash box containing $1, $2, $5, $10, $20, $50 and $100 bills, such that the bills are indistinguishable and the order in which they are selected is unimportant. (there are also at least 5 bills of each kind).  This is like drawing colored balls with replacement. The colors correspond to the values. Since the order doesn’t matter we have: C(7+5-1,5)=
2. A cookie shop has 4 kinds of cookies and we want to pick 6. We don’t care about the order and cookies from one kind are indistinguishable.  Again, drawing colored balls with replacement: colors are kind of cookies. C(6+4-1,6)=84.
3. How many solutions to x1+x2+x3=11 with xi nonnegative integers. This is like throwing 11 balls in 3 boxes. The balls inside each boxe are indistinguishable. C(11+3-1,11)=78.

4.5 Exercise

52 p. 344: How many different cross terms will we generate when we multiply out: (x1+x2+...+xm)^n?  How many different exponents are there of the sort x1^n1 x2^n2 ... xm^nm with n1+n2+...+nm=n. Equivalent to : how many different way are there to put n balls in m boxes: C(n+m-1,n) 38 p.342. Math teacher has 40 issues of a journal and packs them into 4 boxes, 10 issues each. a) How many ways if the boxes are numbered?  assign boxes to issues: 40! / (10!)^ b) Now the boxes are indistinguishable.  There are 4! ways to label the boxes, once we have distributed them in unlabelled boxes. Since the number of ways to distribute them in labeled boxes is given by a) we get 40! / (10!)^4 4!.