Download Fundamental concepts of Tensors and more Summaries Mathematical Physics in PDF only on Docsity!
Temb Arolyis
nneralGeneral uey Snelntiobi.
ongiceum,Hybocbynamis clecuomugne hety
Scalasls amd vecs atepecia Coucs
he quomly svtußbdonel^ chama
i Sialass
Tersotuetahin n^ 3-0? CalledSpace
nvasiemt The (^) 9amlly tohdse^ emunet^ Cha^
urdet elaen^ in^
3D (^) p
is Vecls)V0ient)
rdat 9Lstaten^ n^
D Spo
Terse is^ a^ geembuica^
qyamhly"ashuch^ is^
Sprced bey^
"
9Mcal nwmbexs
anstims into.a^
clepnule
o-tidinale hameimalhen
udr
intoa cleumile c
Nank
Teniea Ce ep
mted dinensiem)
Totalro Copeni
C3) 3 has
nank 1
Temsoh na
3-DpareisiBa
Cempenerk ea. vecl Scaar 3)°
Hamk 0 Tenso in^ a^ 3-0^ pace^
is a has 1rnpenendt
Highox 1Qmk Temst Frank2 Tesot^
n a 3-D^ Space
C
)AshadT CDidinal. uantjonale a,3 harura
shut a
the Rule
o
onura teakpeimalien Og Oga d 0
das
shatCodumte^ tramkjoimal Cwoiduinmte
-idinole barsamaluen A
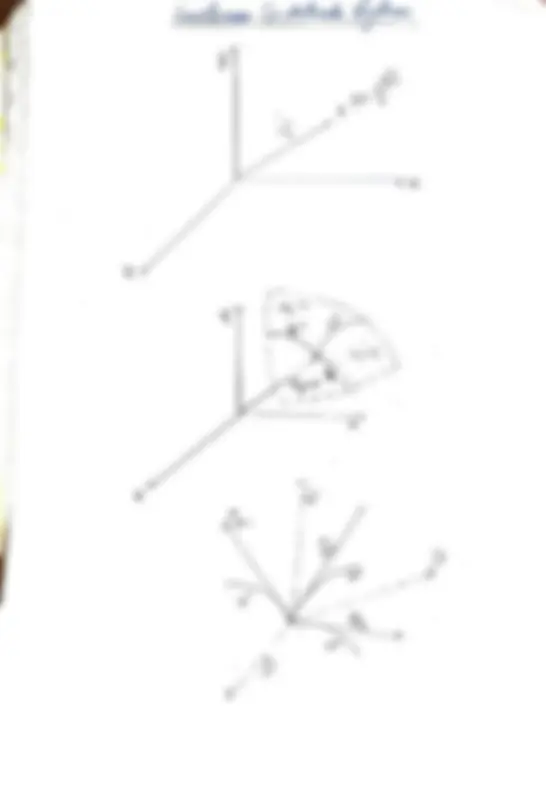
Cersider a^ peind^
in a 3-p Spaca
the poum
In Co-idirie Syplem P
9HepHesemled as^
Pl7,4,3)endP,,)ealp
cyhimdbucad- (P,8, phvoia (7/e,4)
tan () lan
dpet n^ n^
dumesiana (^) Space t8^ pSLL3,emied
neul nurnbes
P(,y) Jn^ an^ unboune^ tn.
CemsicaComsiclex therla-^ D^ 8pace)^ Pou^
P(7,y) n
Xelale the prara ,P(x.
D
in adi clock
Nw (^) CoAdunak Jemud^ is^ P(z^ dR^ b1nd^ (o-inde
han a^ 'n'^ duimensiera^ 6pace^8 sepHesemtec
- Conyes^ i9m^ e^ ,^ urd
~
I 1s 9telaled bybt Co-rdimle^ tramjimlue^ es,^ i
leCe-idinale beaufmalen
(, ,a ) 1,a....
(, , (^) 4mAoülen.T. ) h
heThe - chdtnate said aolmisiade^ Jacebiam^ at
the point PER
anumiabe
sThe Go idinBe tambumaten is 8aio b e Srgubn
Frwod Josheon
dpeint in^ dusmesiena (^) pace in (^) bums .D (^) Spate
Point
F,,(,,) P(X,,P(
di paniall d (^) ds, - d
PEteme (^) Vu tle rkh (^) rolute (^) )rdn (^) rokalin tn (^8) ST(-,x). ae^ the^ (emporunt Torko d rank^ in
-D
Spae A
A (^) A --
Vramhmalion &n^ eters urclun^
yotallen (^) b
T (^) OCCeße+ Sin
NKT
Cenditien -Sire (
Sine+ ohate (^) aa- Sn
A
A
A eTh Jocelsian
A a^ A
CE$0 (^) ( +Sine^ (x)
-y
CetX Sin^8 oc Sine+ e
hom P 8
-s?ne ()^
ce()=x u6^ +^
Sine =
tHhe Compdnenk^
oasos ank^
(^1) in a-p Space (- a
-P Space
Eomovaxiem Teid Raunk-
thesue aare N9yuamlitog ohich ie reprczemkd a
AA Inzf^ o-iclimte^ Syslern^ utah^ js^ Mehsed^
t Na
bhar (^) qyandiss 91epesemted as P^ in^ z}^ co-ddeinne aystem i8^ givem^ by P N 2 A
Pr c In qene
A
thoxe as^ N940mlles^
ch is^ Heprzented^
as
whuih s nelakd
s Covaseicm^ Temso^ Kank
hoys^ in^ fx}^
Co-ddirite Syslem^
huih Telabd^ t
p
ApinTf to-tdinats
ehe 9uantihis^
Tepnegemt as
6pkem i ve N N S
P Ln gemu
Q9le quash^ las^
hch 8 Hepresent s 3elaked to
(^3) Muced Tems Rnk^3 hasre Coddiml
saskem shuih^ s N (^) in lo-oidinal
AT
P
ehor pamlleis
rpresenkd as
sten amd^
qivem 6
A (^) acY
embo algcbra
Rejes to ackktwn tês, Subbaihm Tem
Ceabxaclhin e^ tensos^ ,^ oubr^ poeoduer,^ one^ Axoduct^ amd
ule
dddulaen Temts^ he^ oddduen^ e^6 morc^ frue^ 6ame^ sank
Sum e uo A mote lemsot% ts a lenso e Gamegame A0n
ard ype adelilien uo temcis is Cemmutalire cund ARsoaaure
At s Cerkickr tuuo tonieêk q ku 9ank amdand ypehpe
mP
A
AmP
ieTES bye (a,i) amd ank 3
Qubebaclien _Temkns h Suhadan korss ef sameark
diajrence to é mee erkes ame sank am
ype
Cemidler, B^ tenio^ Iamk^3 ad^ pe^ G
- y o
Addon Qukkocuen uy tennd
S 8
P (^) PN
AtB S
3Paoduuct e nhd6 Tank
he product e uo mds 1s cekeoka cheie preeketed
8u thethe preduct gim lw emries
Pandand tho tup fenkois
Yan
hem P
The eblained^ fots i4^ rank^5
orbachen lonsot
Stuy ene^ Comt^ ravaient^ emmcs^
eqya
met he^ Sesulting^
temd is a^ anbcacdeo^
lemo
hse ank^ Ps^ less^
than a^ tham^ the^ cigiral^ tomot
Yank 5 e 6,a)
BTis drank(5-
Jemo
the
les
PY
et g lemsdo t
ther Y=t^ them
5Tooes Procuc kem
he Outan^ produeF^ Jollouto^ by^
Conbacheo is^ Caled
Inne prodiuc tors A PCU (^8) D (6-)
tha (5-)-^3
rank,
CLest^ D.
bx Proclud^ - Vei^ tha^
fooduch lembds
A B
B1,)o,)
AB
aT G (1,D
A (1, 0) (o
otecnko S 4unCten
CuPlimene Co-idiate yte
P (
u
u-C
,
a
st u Cersfde the
pont (^) PCx,,7) in a
ecangu
he ectanguhs
-0hduiae Sysorm.
T + 4k (^) the pesi hen ecla The Same (^) oindP (^) Ti (^) eporegemled 9n (^) ad ne o-ddinata SuskmSuypem lenimue 9depomdemdalueuu,o, 3 ktxte (^) u'- u'(L 4,7)
u3u(T},
apxedb Cusene
u- C, epmeserda Susats The pesilOD Necta in ne^ Co-eRdumal^ sem^ B^ e)
u', u?,u)
Inkuectu amy tuo^ Sars^ qives
rvedlmes.Thase
LVed Lines^ CemLhh,^ asei^
anecLno-drcle Sugtemm ae thogenas
th inkusechen amay^ u^ SusykaCes
ued ines^ (angti^ tude^
dtcgonal them the eltained then CLevilinaa C-chdinadoSystem
u', u', u,u13)
d T^ dulà¥^ dutY^ du
duo, du^0 o,^ du
9hasta d-~ â,dui Thus Can^ alo^ be^ epyestnrted^
a
ae Collee bas Vecles Thay^ e^ the
tamgmt drauon^
b The^ auxsu,u,^ u^
hane calkd Lan
u, u,^ u3^ honce^ calkd
Hamart bosk vecles
U
hgena vedlsg,^ net^ unt^ vecte
d ?. du (^) d dud - A du' dui at d-^ d?.^ d?
dudu
t
In Caselesiam^ oadimte^ &ystcm:
Tha Co-ddimata^ ane^ i^ n^ by^ u-^
, u'-y u-
i
The maui ksd
Pdd+dx*
Cuimdsica o-didinate Syskem.
u-
S
d de^
sds d
Sphuxical o-diduinale Ssb u
Sina
u'
siso
d dr^ de^
S d
Minkouke 3pace
u
u ut ict
obtain the^ Cenugale^ mabuc fess^ in^ isbeical^ and pelav. Co-drcdindles. lindvi cal amd the
g
1/ kT (^) O O -ac_ DKT (^) (enugate mabic^ femsdh dt( 3-0) -0+0 3* 9s-jads O ) Feh^ Sphtiral^ to-^ hdimate^ Sskem.^ (oah Sio'e
