Download Series RLC Circuit: Power and Resonance and more Study notes Physics in PDF only on Docsity!

1

Lecture 43 – Electromagnetic oscillations^ •^

Review

-^

The series RLC circuit

-^

Power in RLC circuits

-^

Transformers

2

Review

• Alternating

Emf

• Simple alternating current circuits

)

sin(

sin^ φ ω

ω

ω −

=

= =

t

I i

A B N

Emf

t

Emf

Emf

d

d

m

d

m 0 0

φ

ω

φ

ω

φ d L L L L d

C

C C C

R R

L

X

X

I

V

C

X

X

I

V

R

I

V

4

The Series RLC Circuit

L

X

XI

V

C

X

XI

V

RI

V

d L L L

d C C R C

2

2

2

)

(^

C L R m^

V V V

Emf

−

=

[^

2 ]

2 2 2

2

2

(^

C L

C L

m^

X

X

R

I

XI

XI

RI

Emf

defined)

(impedance

)

(

2

2

2

2

C L

m

C m L

X

X

R

Z

EmfZ

X X R

Emf

I

amplitude)

(current ) / 1

(^

2

2

C

L

R

Emf

I

d

d

m

ω^

−

=

5

resonance

X

X

inductive

than

capacitive

more

X

X

capacitive

than

inductive

more

X

X

C L

C L

C

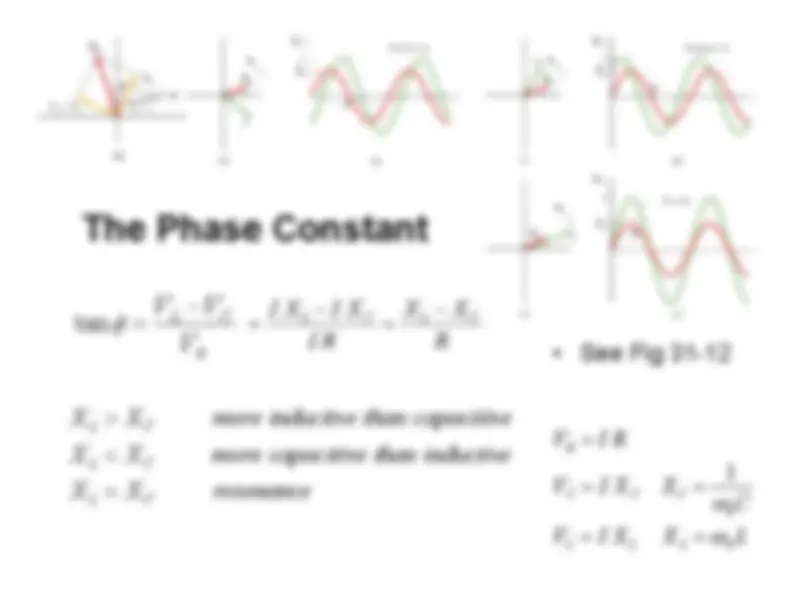
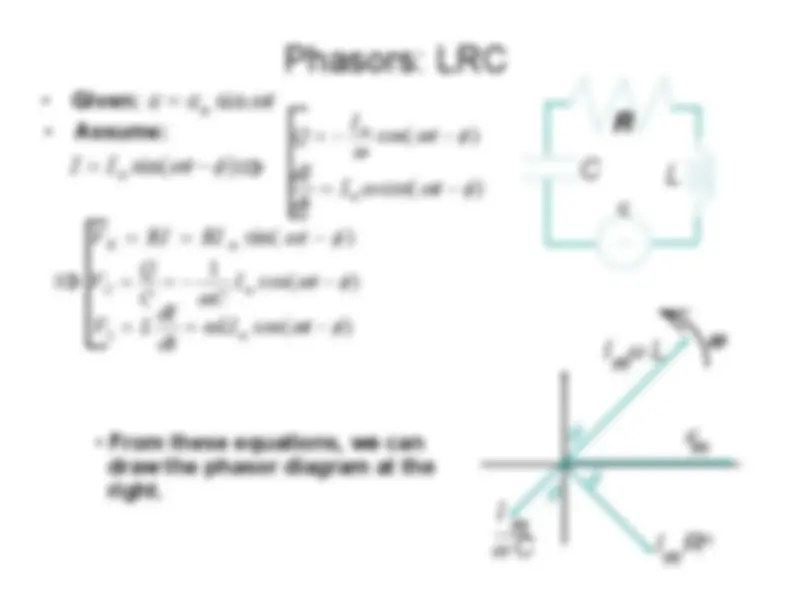
The Phase Constant > L <^ =

-^

See Fig 31-

R

C L V

V V^

−

φ tan

L

X XI V

C

X XI V

RI V

d L L L

d C C R C

ω ω=

=

=

= =

1

X R X

RI

XI XI

C L C L^

−

−

=

7

What is

reactance

You can think of it as a frequency-dependent resistance.

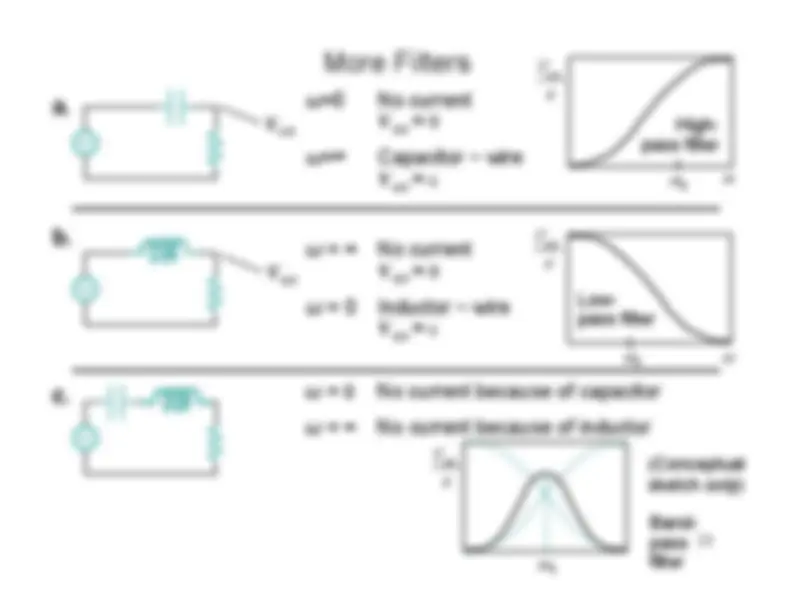
For high

ω ,

χ C

• Capacitor looks like a wire (“short”)

For low

ω ,

χ C

Æ∞

• Capacitor looks like a break

1

X^ C

C ω

For low

ω ,

χ L

• Inductor looks like a wire (“short”)

For high

ω ,

χ L

Æ∞

• Inductor looks like a break (inductors resist change in current)

X^ L

L ω=

( "

"^

)

X^ R

R

8

Resonance

The current in an LRC circuit depends on the values ofthe elements and on the driving frequency through therelation

Im

0 0

2ω

o

ε m R^0

R =

Ro R =

Ro R

XL XC

Z

XL^

-^ X

C

Plot the current versus

ω, the

frequency of the voltagesource:

→

X R

X^

C

− L

=φ

tan

cos

φ

R

I^

m

m

ε

Z

I^

m m

ε

φ R cos Z^

=

10

Checkpoint 31-

Here are the capacitive reactance and the inductive reactance,respectively, for three sinusoidally driven series RLC circuits: (1) 50 Ω, 100

. (a) For each, does the

current lead or lag the applied emf, or are the two in phase? (b) Whichcircuit is in resonance?

X R

X^

C − L

tan

tan

=^

R

R

X R

X^

C L φ

lags

current

φ

φ

tan

=^

R

R

X R

X^

C L φ

leads

current

φ

φ

tan

=^

R

X R

X^

C L φ^

resonance

0

⇒

sin(

sin(^ φ

ω

ω

t

I

i

t

Emf

Emf

d

d

m

11

Power in LRC Circuit

-^

The power supplied by the

emf

in a series LRC circuit depends

on the frequency

ω. It will turn out that the maximum power is

supplied at the resonant frequency

ω^0

•^

The instantaneous power (for some frequency,

ω ) delivered at time

t^ is

given by:

-^

The most useful quantity to consider here is not the instantaneouspower but rather the average power delivered in a cycle.

-^

To evaluate the average on the right, we first expand the

sin

(^ ω t

-^ φ

term.

(^

)(^

))

sin(

sin

)( )( )(

φ ω

ω ε

ε^

−

=

=^

t

I t

tI t t P^

m

m

Remember whatthis stands for

〉 −

〈

=〉

〈^

)

sin( sin

)(

φ ω ω

ε^

t t

I

t P^

m m

13

Power in LRC Circuit

-^

This result is often rewritten in terms of rms values:

m

rms

ε^

1 2 ≡^

m

rms^

I

I^

φ

ε^

cos

rms rms

I

t

P^

•^

Power delivered depends on the phase,

φ,^ the “power factor”

•^

Phase depends on the values of

L ,

C ,

R ,

and

•^

Therefore...

14

Power in RLC

-^

Power, as well as current, peaks at

ω^

=^ ω

. The^0

sharpness

of the resonance depends on the values of the

components.

-^

Recall:

φ

ε^

cos

)(

rms rms^

I

t P^

=〉

〈^

ε^

cos

R

I^

m

m^

-^ Therefore,

2

2

(^2) rms

( )

cos rms

P t

I^

R

ε^ R

φ

〈^

〉 =

=

We can write this in the following manner (which we won’t try to prove):

2 2 2 2

2

2

) 1 (

)(

−

=〉 〈^

x Q x

x

R tP

ε rms

…introducing the curious factors

Q^

and

x ...

16

Power in RLC

0 0

2ω o

2 rms R^0 ε

R =

Ro R =2 R

o

Q =

FWHM

For

Q^

> few,

fwhm Q^

ω res ≈

17

FWHM and

Q

• FWHM

–Full Width Half Maximum

-^

Q^ – Quality of the peak^ – Higher

Q

= sharper peak = better quality^

0 0

2ω o

2 rms R^0 ε

R =

Ro R =2 R

o

Q =

FWHM

19

Problem

-^ What is the relation between

P I

and

P II

, the power delivered by

the generator to the circuit when each circuit is operated at itsresonant frequency?(a)

P

<II P

I^

(b)

P

=II P

I^

(c)

P

>II P

I

-^ Consider the two circuits shown where^ 2A 2B •^ At the resonant frequency, the impedance of the circuit is purely resistive. •^ Since the resistances in each circuit are the same, the impedances at theresonant frequency for each circuit are equal. •^ Therefore, the power delivered by the generator to each circuit is identical.

C II

= 2

C .I

• What is the relation between the qualityfactors,

Q I

and

Q II

, of the two circuits?

(a)

Q

<II Q

I^

(b)

Q

=II Q

I^

(c)

Q

>II Q

I

L C R ε^ ∼

L C R ε^ ∼

I^

II

20

Sample Problem 31-

A series RLC circuit, driven with

Emf

rms

= 120 V at frequency

fd^

Hz, contains a resistance R = 200

, an inductance with X

= 80L

, and

a capacitance with X

= 150C

.^ (a)

What are the power factor

cos

φ^ and

phase constant

φ^ of the circuit?

R = Z φ cos

2

2

)

(^

C L^

X X R Z^

−

=

=^

2

2

2

2

C L^

X

X

R

Z

a

(^3). 19 (^944). 0 cos

(^944). 0 (^9). (^200211)

cos

1

±=

= ⇒

=Ω Ω = =^

− φ

φ^

R Z

(b)

What is the average rate P

at which energy is dissipated in theav

resistance?

C L^

X

X^

φ

cos

rms rms

av^

I

Emf

P^

=^

EmfZ

I^

rms

rms^

(^

)^

W

V

Z

Emf

EmfZ

Emf

P^

rms

rms rms

av^

cos

cos

2

2

φ

φ