




























































































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Two models for urban development: the inter-urban model, which describes the evolution of urban centers within a region, and the intra-urban model, which describes the structural evolution of an urban center. The authors also explore the significance of transportation choices and the impact of different decisions on the global evolution of the system. The document also introduces a Boolean formalism for modeling complex systems.
Typology: Study notes
1 / 122

This page cannot be seen from the preview
Don't miss anything!





























































































P.M. Allen J.L. Deneubouro M. Sanglier - F. Boon A. de Palma
University of Brussels Brussels, Belgium
DOCUMENTTHROUGH THE IS AVAILABLE NATIONAL TOTECHNICAL THE PUBLIC INFORMATIONVIRGINIA 22161 SERVICE, SPRINGFIELD,
Prepared for U.S. DEPARTMENT OF TRANSPORTATION RESEARCH AND SPECIAL PROGRAMS ADMINISTRATION Office of Transportation Programs Bureau Office of Systems Engineering. Washington DC 20590
This document is disseminated under the sponsorship of the Department of Transportation in the interest of information exchange. The United States Govern- ment assumes no liability for its contents or use thereof.
The United States Government does not endorse pro- ducts or manufacturers. Trade or manufacturers' names appear herein solely because they are con- sidered essential to the objec.t of this report.
The dynamic urban growth models discussed in this report build upon research begun in 1976 and reported on in the U.S. Department of Transportation Report No. DOT-TSC-RSPA-78-20.I, II October 1978. In this previous report we de!eloped two models: the inter-urban model which describes the evolution of urban centers within a region, and the intra-urban model which describes the structural evolution within each center. This report presents a further extension of these models including an analysis of an urban system's dynamic, "collective" organization. Section 3 of this report on dynamic models of competition between transportation modes has also been published in Environ- ment and Planning International Journal of Urban and Regional Research, Volume II, 1979 co-authored by J.L. Deneubourg and A. de Palma from the University of Brussels and D. Kahn from the Transportation Systems Center.
The technical monitor, D. Kahn, of the contract under which this work was performed would like to take this opportllility to acknowledge the copy and production editing of Caron Tsapatsaris for this report.
iii
Section
The Behavioural Equations 30 The Decision Variables 34 Th~ Collective Structures, Projected into a Theoretical City 37 The Comparison of the Theoretical City with a Real City 52 2.3 Boolean Formalism, -a Tool for Decision Making? 57 2.3.1 A General Development Policy or the Search for Coherence Between Goals and :Means............................. .. 60 2.3.2 The Planning of a Specific Neighbourhood or the Search for the Best Strategy of Investments.. •........................ .. 62 NOTES AND REFERENCES ....•........................... 70
Introduction ;................ .. 75 Development of the Dynamic Equations 76 The Theoretical Models 77 Conclusions 94 REFERENCES........................................ .. 95 APPENDIX.......................................... .. 96
v
Figure
TOO ".. 1,1 • •• • • • • • • •• 11
DECAY , '..... • ..•... 12
vi
Figure Page
viii
Figure
ix/x
This report describes the further development and exploration of the dynamic models of urban evolution for which the basic methodology was laid down in work performed by our group under a previous contract (TSC-1185 - Final Report).l These methods are derived from new concepts that have recentiy emerged in the physi- cal sciences in connection with the discovery of "dissipative structures" 2 , 3. These occur in physical systems having elements which interact in a non-linear manner, involving positive and negative feedback loops, and which are open to the exterior, exchanging matter and/or energy with the outside world, and in this way remaining far from thermodynamic equilibrium. The evolution of such systems involves both deterministic stab~e periods, as well as bifurcation points in the vicinity of which instabilities occur, when "fluctuations," small local inhomogeneities, are amplified and carry the system to some new, qualitatively different state of organization. This process of "order by fluctuation" is of great generality for the evolution of complex systems, and applies to systems composed of basic units which are themselves already macroscopic objects containing mechanisms governing their interactions with the environment and with the other elements of the systems. Thus, given some basic "behaviour pattern" of the individual elements, their mutual interaction can lead to a self-organization of the system through successive instabilities of the collective structure.
describing the evolution of urban centers within a region, the inter-urban model, and the other describing the structural evolution of an urban center, the intra~urban model. In this report we describe the further extension of these models at the level of dynamic organization~ and also in the direction to the "collective" aspects of the behaviour patterns" used to describe consumer choice, for example, in the urban system. As
xi
we shall see, the modelling of the dynamic evolution of the urban system entails the description of a collective organization 'Which results from the mutual interaction of the behaviour patterns of the various populations, which may in their turn reflect a "collective organization" at a lower level as the individuals within the popUlations, interact. The situation is one of insta- bilities within instabilities and so on!
In the first section the inter-urban model is modified so as to give a much more realistic representation of the evolution of the urban centres of a region, where large centers sprawl outwards forming residential suburbs. The modified version of the model now corresponds to a picture of the evolution of a region wherein we not only have the formation of an interacting hierarchy of urban centers, but also one in which there. is an internal struc- tural evolution within each center. Only such a model can assess the real global effects of a modification,forexample, in the transportation system within a partiCUlar urban center.
The second section is devoted to the development of a new method which offers the perspective of an enormous simplification and saving of time in the analysis of a urban evolution. It is a method based on the techniques of Boolean algegra, in 'Which con- tinuous variables are replaced by discrete ones, the yes/no, 0/1, of the binary system. Boolean algebra has been applied in the first instance, to the evolution of the internal structure of a city. By describing the "presence" or "absence" of a given popUlation according to 'Whether it is above or below a certain percentage of the local residents, the very large number of distinct stationary states which may characterize the continuous variable differential equations of intra-urban structure , is reduced remarkably to those which can be distinguished according to the threshold criteria chosen. Furthermore, the "dynamics" of such a problem consist in the assignment of probabilities for the passage from one stationary state to another, and this is simplified to a problem of time-delays. It is assumed that a "change" 'When it occurs, concerns only one variable at a time,
xii
we can have more than one stable stationary state, in the vicinity of which the collective reaction of users to any slight deviation from this state, is negative. That is to say that the response of the users is such as to damp any small perturbation of this ratio for the modal split fractioning of users. Nevertheless, it is still possible that these stable stationary states corres- pond to very different levels of global "satisfaction," but that some large scale Te-organizationis required in order to leave the less favourable stable state. This is clearly an important feature for planning decisions, and also for the implications of inter-modal competition for the evolution of urban structure. As the urban structure evolves, travel demand between various points in a city can exceed or fall below thresholds which can lead to a sudden, discontinuous, change in modal use, and hence in trans- port "costs." Any integrated model of the global effects of transport investment, for example on the urban structure and economy, must take such factors into account. The integration of these three separate aspects that are the subject of this report will have to be left for. the future when general equations may be written down which encompass all these different elements, and which reduce to the various simpler equations under well defined assumptions. The equations for the inter-urban evolution are being tested by an application to the time evolution of the urb~ hierarchy of the Bastogne region of Belgium, and clearly the Boolean methods of the second section can be extended to this model as well. Similarly, the section devoted to intermodal competition is also reI event to ~n inter-urban model where apart from the various modes of passenger travel, there are also those available·to the transport of merchandise, (airlsea/rail/road/pipeline). Also this third section raises the question of the relation between the models which we have described here Land in our previous report), and various other methods of urban and economic modelling (global utility functions; optimization techniques; Pareto maxima; entropy maximization etc.). The clarification of this relation
xiv
should lead to a much more thorough understanding of the real significance and status of these various methods, which in turn lead to the establishment of a much more solid foundation to a "theoretical social dynamics," and hence to the problems of evolving urban systems.
xv
In our previous reports a dynamic version of central place theory was developed based on the mutual interaction of the spatial distributions of population and emplo}Jnent. This inter- action constituted a positive feedback, which, when the effects of fluctuations are included explicitly, leads to a self-organi- zation of the system into an urban hierarchy which reflects the the dual effects of historical chance and economic necessity. This introduces the possibility of describing qualitative changes in the spatial organization of a region, changes which ususlly mark the breakdown of previously successful extrapolations in the behaviour of the system. Our model consists of two sets of equations, one for the population of each point i, x., and the other for the growth and decay of economic functions k~ at each point i, S.(k). ~ In the equation for x., ~ the population responds to the employment opportunities at the point i,
dx.~ dt = bx. ~^ (N^ +^ kIS. ~^ (k)^ -^ x.)~^ -^ mx. ~^ (1)
where band m are related to the birth and death rates respective- ly as well as to the mobility of the population. N represents the "natural" carrying capacity of each point of the system in the absence of economic exchange between different localities.
fhe different economic functions situated there.
to the economic demand that is attracted to the point i,
dS. Ck) ~ at =^ ex^
S. (k) ~^ (Demand^ for^ k^ at
1
i - (2)
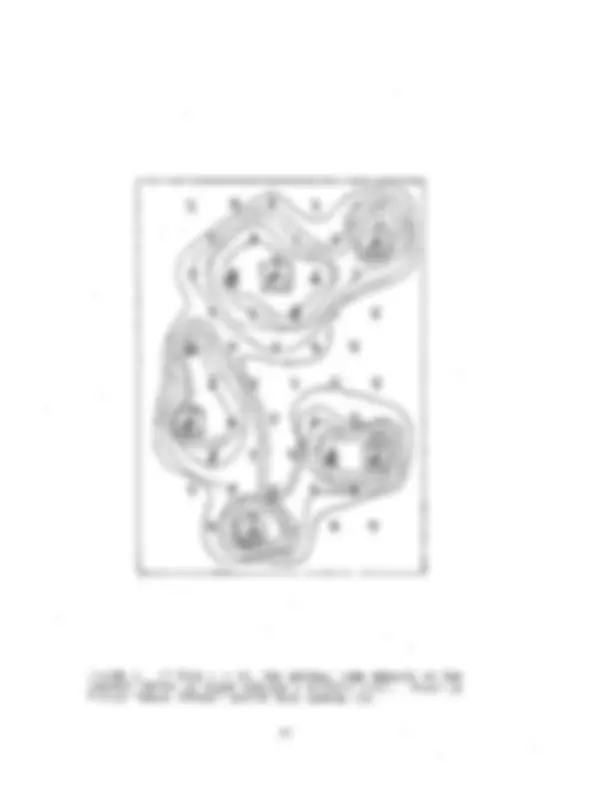
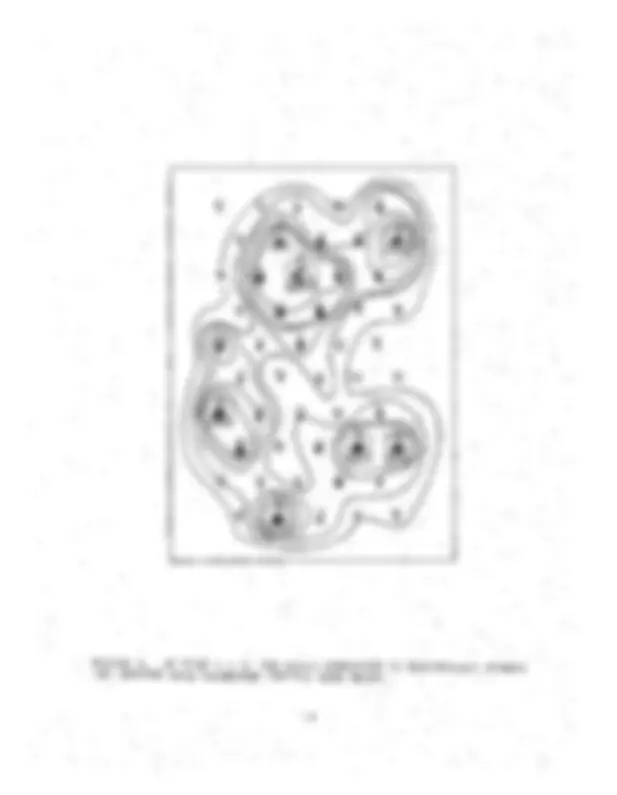
The demand arriving at the point i for the ·function k is then related to the "attractivity" of the point i to each population x.J at j, relative. to that of others offering the function k. We shall return to this point ~ater. ·The other important feature of our model was the random appearance of economic functions at different points in the system. The first model was as general as possible, and the probability of the launching of a particular function was taken as being uniform over the whole region. In any given experiment, however, a particular sequence occurs and this leads to a distri- bution of urban centers following the growth of some centers and the elimination of others according to the economic laws contained in equations (1) and (2). Typically, we have a result such as is shown in Figure 1 after the stochastic launching of two economic functions. At each point we a~readyhavedomesticfunctions,and the two new func- t~ons concern economic interaction between the points, of medium and long range respectively.
Although as we see from Figure 1 the equations (1) and (2) give rise to a reasonable form for the distribution·of centers; there is an important mechanism missing from our description: the competition for space that will occur at a given point. That is to say that in equations (1) and (2) we have assumed that employment and residences can be stacked on top of one another without limit at a given locality. The number of jobs divided by the number of residents, a r:atio known as the coefficient of employment, is equal to unity for each point separately. One of the improvements that we shall describe here is therefore the correction of this inadequacy in the simplest possible manner. We sha~1 suppose that with a certain probability, as the effects of crowding become· more intense, a certain fraction of thepopu- lation decides to reside on the points neighbouring that of its place of employment. This is represented by adding two terms into equation (1), which express the idea that for every "route" out of an urban center a fraction of the population having
2