Assignment – Module 4
1. Determine the autocorrelation at lag 3 for the data given below. Check if this correlation
is significant at 95% confidence level.
14,000 17,700 17,500 15,500 20,500 18,100 15,800 14,900 16,300
14,900 17,600 17,000 17,300 18,300 19,100 17,900 19,400 22,900
16,200 14,300
2. For the data given below, estimate the spectral densities for p=1,2 and 3 with notations
followed in the lectures, for a maximum lag of 2
Year
1
2
3
4
5
6
7
8
9
10
11
Peak flow
(m3/sec)
2160 3210 3070 4000 3830 978 6090 1150 6510 3070 3360
3. Statistical properties (in Mm3) of streamflow at a site in the three seasons of a year are
given below
___ ___________________________________
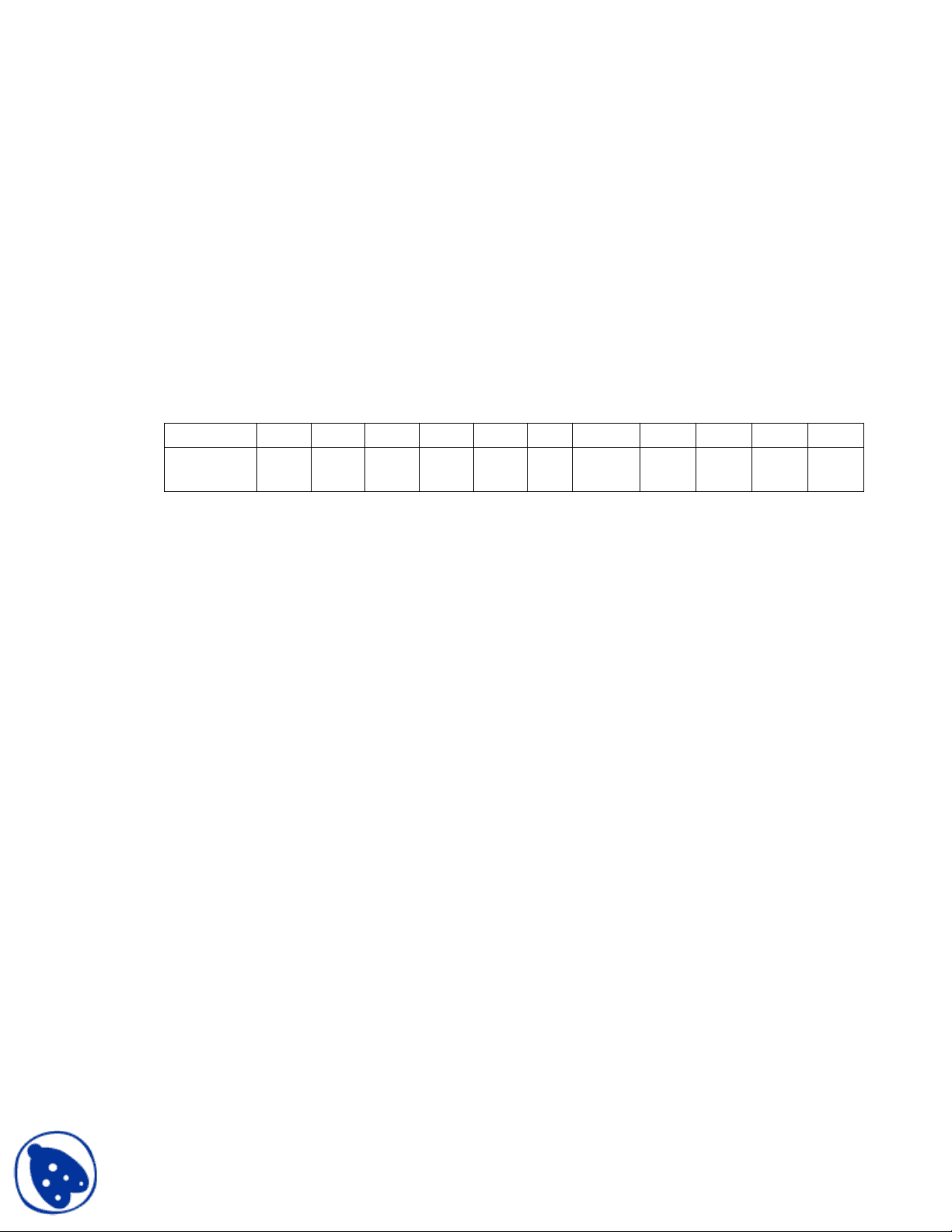
Season I Season II Season III
______________________________________
Mean 35 15 8
Std. Devaition 40 10 6
Lag one
Correlation 0.43 0.67 0.5
______________________________________
The lag one correlation is the correlation of flows with those of the previous season.
Using a Non-stationary, First Order Markov Model, generate streamflow data for 3 years
at the site. State the assumptions you make in using such a model.
4. Given the auto-correlations, r1 = -0.671 and r2 = 0.463, obtain the initial estimates of
parameters of an ARIMA (2,1,0) model using Yule Walker equations.
Docsity.com
