Download Cross Products and Moments of Force ( ) ( ) and more Study notes Statics in PDF only on Docsity!
Cross Products and Moments of Force
Ref: Hibbeler § 4.2-4.3, Bedford & Fowler: Statics § 2.6, 4.
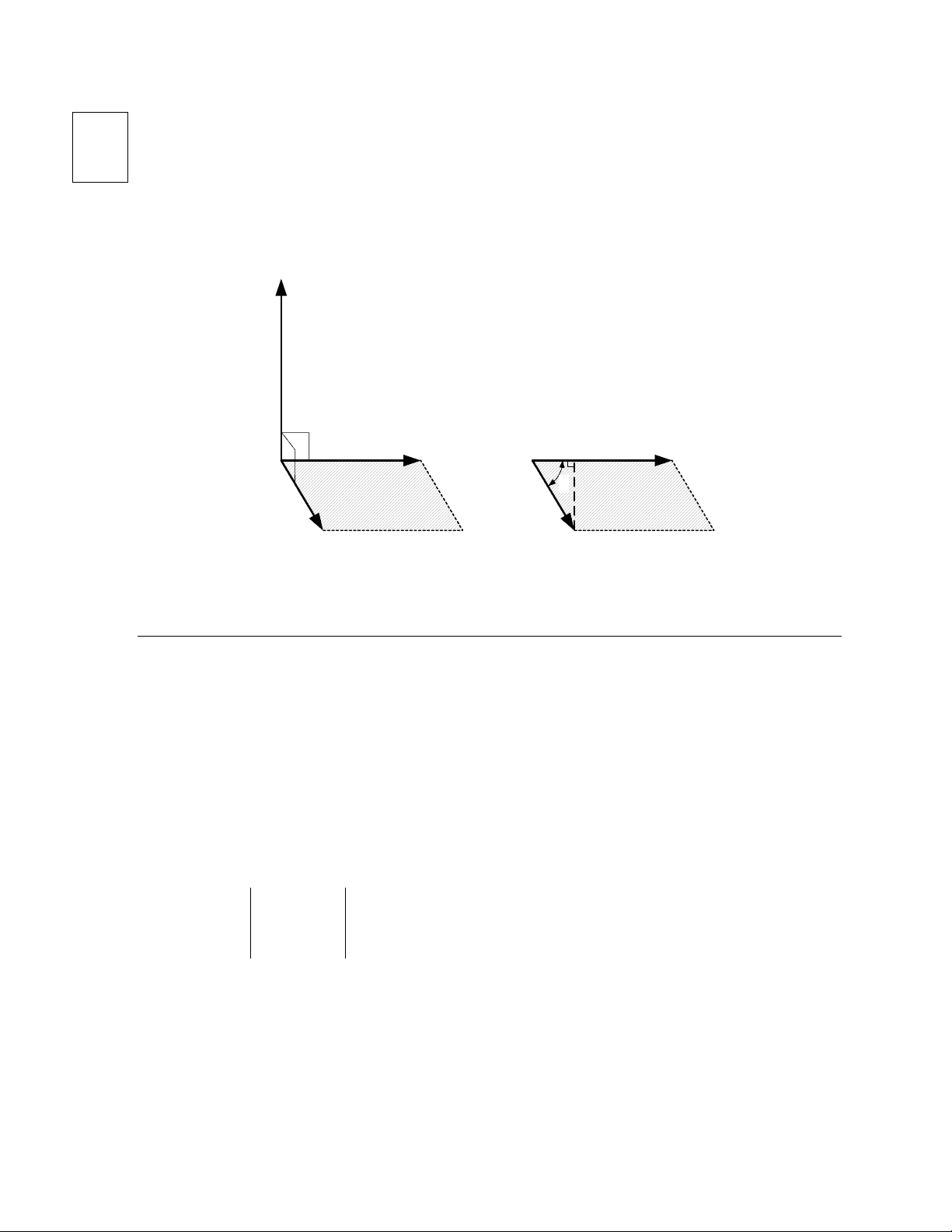
In geometric terms, the cross product of two vectors, A and B , produces a new vector, C , with a direction perpendicular to the plane formed by A and B (according to right-hand rule) and a magnitude equal to the area of the parallelogram formed using A and B as adjacent sides.
A
B
C
A
B
θ A sin(θ)
Area = A B sin(θ)
The cross product is used to find the moment of force. An example of this will be shown after describing the basic mathematics of the cross product operation.
The cross product (or vector product) can be calculated in two ways:
- In trigonometric terms, the equation for a dot product is written as
C = A × B = A B sin( θ) u C
Where θ is the angle between arbitrary vectors A and B , and u C is a unit vector in the direction of C (perpendicular to A and B , using right-hand rule).
- In matrix form, the equation is written in using components of vectors A and B , or as a determinant. Symbols i , j , and k represent unit vectors in the coordinate directions.
( ) ( ) ( )
x y z
x y z
y z z y x z z x x y y x
B B B
A A A
A B A B A B AB A B A B
i j k
A B i j k
× = − − − + −
MATLAB provides a cross product function to automatically perform the calculations required by the matrix form of the dot product. If you have two vectors written in matrix form, such as
A = (1, 2, 3)
x
y
B = (-1, -2, -1) z
Then A × B can be calculated like this (bold letters have not been used for matrix names in MATLAB):
» A = [1 2 3];
» B = [-1 -2 -1];
» A_x_B = cross(A,B) %Uses MATLAB’s cross product function
A_x_B =
4 -2 0
To verify this result, we can do the math term by term…
» x = 1; y = 2; z = 3; %Coordinate index definitions
» [ A(y)B(z)-A(z)B(y) -(A(x)B(z)-A(z)B(x)) A(x)B(y)-A(y)B(x) ]
ans =
4 -2 0
Or, we can use the trig. form of the cross product. First, we calculate the norm, or magnitude, of the A and B vectors using the norm function in MATLAB…
» A_mag = norm(A)
A_mag =
» B_mag = norm(B)
B_mag =
Then find the angle between vectors A and B using MATLAB’s acos() function.
» theta = 180/pi * acos(dot(A,B)/(A_mag * B_mag))
theta =
The magnitude of the C matrix can then be calculated…
Annotated MATLAB Script Solution
%Define the vectors A = [1 2 3]; B = [-1 -2 -1];
%Take the cross product A_x_B = cross(A,B); fprintf('A x B = [ %1.4f %1.4f %1.4f]\n\n', A_x_B)
%Check MATLAB's cross product operator by calculating the cross product explicitly... x = 1; y = 2; z = 3; % Define coordinate index definitions A_x_B_exp = [A(y)B(z)-A(z)B(y) -(A(x)B(z)-A(z)B(x)) A(x)B(y)-A(y)B(x)]; fprintf('A x B calculated explicitly= [ %1.4f %1.4f %1.4f]\n\n', A_x_B_exp)
%Use the trigonometric form of the cross product operator to find the magnitude of the C vector. % First, find the magnitude of the A & B vectors using the norm function. A_mag = norm(A); B_mag = norm(B); fprintf('Magnitude of vector A = %1.4f \n', A_mag) fprintf('Magnitude of vector B = %1.4f \n', B_mag) % Then, find the angle between vectors A and B. theta = 180/pi * acos(dot(A,B)/(A_mag * B_mag)); fprintf('Angle between vectors A and B = %1.4f deg\n', theta) % Finally, solve for the magnitude of the C vector. C_mag = A_mag * B_mag * sin(theta * pi/180); fprintf('Magnitude of vector C = %1.4f \n\n', C_mag)
%Solve for the direction of the C vector cross(A,B)/norm(cross(A,B)); % or C/C_mag where C = cross(A,B)
alpha = acos(0.8944) * 180/pi; beta = acos(-0.4472) * 180/pi; gamma = atan(0) * 180/pi; fprintf('alpha = %1.4f deg from +x\n', alpha) fprintf('beta = %1.4f deg from +y\n', beta) fprintf('gamma = %1.4f deg from +x\n', gamma)
%Plot the A, B, and C Vectors x = [ 0 0 0; 1 -1 4];
y = [ 0 0 0; 2 -2 2];
z = [ 0 0 0; 3 -1 0];
plot3(x,y,z,'-o','LineWidth',2,'MarkerSize',5); set(gca,'FontSize',18) grid; xlabel('x-axis'); ylabel('y-axis'); zlabel('z-axis'); legend('C-blue','B-green', 'A-red',2);
Example: Find the Moment of a Force on a Line
A force of F = 200 N acts on the edge of a hinged shelf, 0.40 m from the pivot point.
M_mag =
However, the moment of force F about the x axis requires an additional dot product with a unit vector in the x-direction, and is found as
» u_x = [1 0 0];
» M_L = dot(u_x, cross(r,F))
M_L =
-62.
The minus sign indicates that the moment is directed in the –x direction.
Solution Using Scalars
The moment of force F about the x axis can also be determined by multiplying the y-component of F and the perpendicular distance between the point at which F acts and the x axis.
ML = Fy d
Since the component of F in the y-direction is known (157 N), and the perpendicular distance is 0. m, the moment can be calculated from these quantities.
» d = 0.40;
» M_L = F(2) * d
M_L =
The direction must be determined using the right-hand rule, where the thumb indicates the direction when the fingers are curled around the x axis in the direction of the rotation caused by F (^) y.
Annotated MATLAB Script Solution
%Define the vectors r = [0 0 0.4]; F = [-40 157 118];
%Take the cross product of r with F to get the moment about point 0 (the origin); M_o = cross(r,F); M_mag = norm(M_o); fprintf('M_o = r x F = [ %1.4f %1.4f %1.4f]\n', M_o) fprintf('M_mag = |M_o| = %1.4f\n', M_mag) %Note: This is not the solution to the stated question. % The question asks for the moment about the x axes. % That will be calculated next
%Declare a unit vector in the x-direction in order to calculate the moment about the x axis. u_x = [1 0 0];
%Calculate the moment about the x axis M_L = dot(u_x, cross(r,F)); fprintf('Moment about the x axis = %1.4f\n', M_L)
%Check the results using scalar math d = r(3); M_L = F(2) * d; fprintf('Moment about the x axis (with scalar math) = %1.4f\n', M_L)
