Generating Functions and Counting Combinations, Slides of Discrete Mathematics

Download Generating Functions and Counting Combinations and more Slides Discrete Mathematics in PDF only on Docsity!

Lecture 17

Generating Functions

Recap

0 1 0

( ) ... ...

k k k k k

G x a a x a x a x

∞

=

Generating functions are defined by a sequence as follows:

Thus: For every sequence there a generating function and for

every sequence there is a generating function.

Idea: Use properties of functions to solve problems about sequences.

Recap: Extended Binomial Coeff.

0

(1 ) , , | | 1

u k

k

u x x u R x R x k

∞

=

 

• = (^)   ∈ ∈ <  

∑

( 1)( 2)...( 1) , !

1 0

u (^) u u u u k if u R k Z k k

u if k k

  − − − +  =^ ∈^ ∈^ +  

   =^ =  

The binomial theorem was extended to real values for u, using the definition of extended binomial coefficients.

Application to Counting Problems

What is the number of r-combinations from a set with n elements when repetition is allowed?

I.e. in how many ways can we pick r element from a bag of n elements, when the supply of these elements in infinite (imagine we replace the elements).

n colors

r indistinguishable slots

the balls are replaced when they have been drawn

Docsity.com

r-Combinations with repetion

2 3

0

0 0

0

1 ( ) (1 ...) 1

(1 ( )) ( )

( 1) ( 1, )( 1) ( 1)

( 1, )

n n

n k

k

k k k k k

k k

k

k

G x x x x

n x x k

n x C n k k x k

C n k k x

∞ −

=

∞ ∞

= = ∞

=

  = + + + =    − 

 −  = + − = (^)   −  

 −  = (^)   − = + − − −  

= + −

Now let’s compute that coefficient:

Looks familiar?

r-combinations without repetition

the balls are not replaced when they have been drawn

X

X

X

X

r indistinguishable slots

n colors

(1+x)

(1+x)

(1+x)

(1+x)

(1+x)

(1+x)

A ball can only be used once, thus it is there or it is not there in the collection of slots.

x x x x 1 1 = x^

The number of r-combinations of a set with n elements without repetition is therefore

equal to the coefficient in front of the generating function G(x)=(1+x)^n Docsity.com

Counting with constraints

Now let’s say, we want to make sure that we pick r elements out of n with repetition allowed, but we want at least 1 element from each kind:

G(x) = (x+x^2+x^3+...)^n

We are looking for the coefficient of x^r.

2 3

2

0

( ) ...

(1 ...)

1 1

( 1, )

( 1, )

n

n n

n n

n k k

j j n

G x x x x

x x x

x x

C n k k x

C j j n x

∞

= ∞

=

= + + +

= + + +

  = (^)    − 

= + −

= − −

∑

∑

Here we used the calculation of a few slides back.

Here we redefined: j=n+k

Note that choosing less than n objects is not possible!

Solving Recurrence Relations

1 0

0 0 1 0 0 1 1 0

0 0 0 0

3 2.

( ) 3 3 3 ( )

( ) 3 (2 3 ) 1 3

k k

k k j k k j k k j

k k k k

k k

a a a

G x a a x a a x a x a x a xG x

a G x a x x x

− ∞ ∞ ∞

− = = = ∞ ∞

= =

= =

= + = + = + = + ⇒

= = = × −

therefore we have found that a[k]=2x3^k is the solution!

6.5 Inclusion-Exclusion

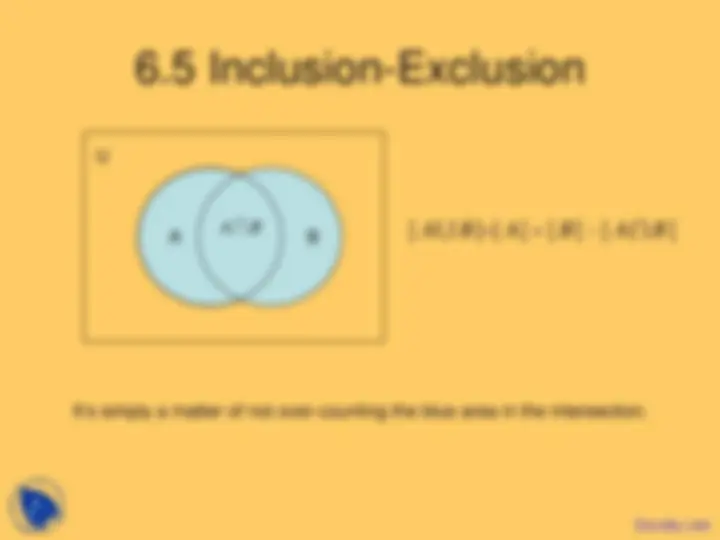
A (^) A B

U

A  B | A  B | |= A | + | B | −| A B|

It’s simply a matter of not over-counting the blue area in the intersection.

Now three Sets

A B

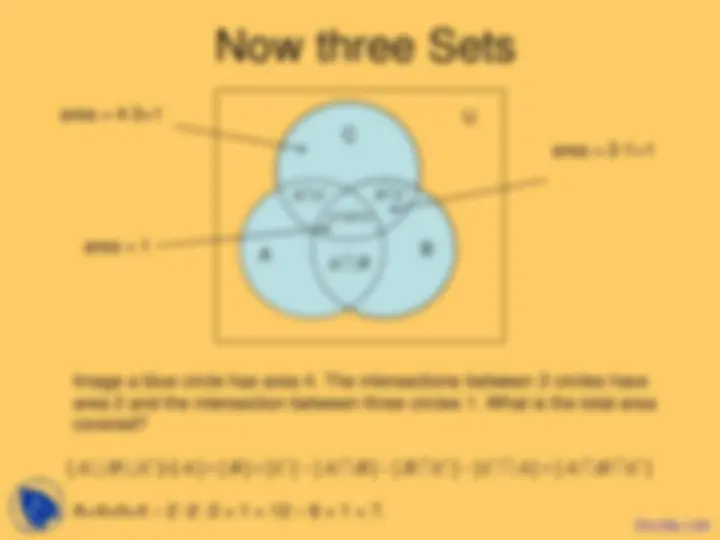
C

A B

A  C B^ C A  B C

U

Image a blue circle has area 4. The intersections between 2 circles have area 2 and the intersection between three circles 1. What is the total area covered?

A=4+4+4 – 2 -2 -2 + 1 = 12 – 6 + 1 = 7.

area = 2-1=

area = 1

area = 4-3=

| A  B  C | |= A | + | B | + | C | − | A  B | − | B  C | − | C  A | +| A  B C|