Download basic mathematics of measurement and more Slides Engineering Mathematics in PDF only on Docsity!
CHAPTER 3
SOLID GEOMETRY: CONCEPTS AND APPLICATIONS
3.1 Basic Concepts of Solids 3.2 Measurements of Solids The world around us is obviously three-dimensional (Euclidean space) having height, width, and depth. Understanding solids is a building block for finding their lateral area, surface area, and measurements of volumes of various solid figures. These include pyramids, cylinders, cubes, cones, spheres and prisms. In this chapter, we will discuss some solids with their corresponding formulas for finding volumes, surface areas and its application to practical problems used in real life. The solids that are included in our study are cubes, rectangular parallelepiped, prism, cylinder, pyramid, cone and sphere. Below are the descriptions of the terms used in our study of solids. M At the end of the chapter, students are expected to ๏ท Identify different geometric solids. ๏ท Explore the properties and attributes of two and three dimensional figures. ๏ท Apply the concepts of geometric solids to various real-life problems in the world around them. Vertex Section Face Edge Base
A C
B
E D
3.1 Basic concept of Solids A solid is any limited portion of a space, bounded by surfaces. Not hallow inside. Figures can be classified according to their dimensions. Two-dimensional figures are plane figures, or โflatโ figures. A plane figure is a flat figure that does not have depth to it. Here are some examples of plane figures. Here you have a circle, a triangle and a rectangle. You can see that these figures have been created on one plane. They are two-dimensional figures. Then, there are three-dimensional figures or solid figures. Solid figures are not limited to one plane and have depth. There are many different types of solid figures. Illustration:
- Draw an octagon and identify the edges and vertices of the octagon. How many of each are there?
- Find the area of a square with 5 cm sides.
- Draw the following polygons. a. A convex pentagon. b. A concave nonagon.
Parts of a Solid
1. Polyhedron - is a solid bounded by planes.
2. Faces - are the portions of the bounding
planes enclosed by the edges.
3. Edges - are the intersections of the
bounding planes in a polyhedron.
4. Vertex/Vertices - are the intersections of
the edges.
5. Section - of a solid is the plane figure cut
from the solid by passing a plane through
it.
Vertex Section Face Edge Base
A C
B
E D
3.1.1a Prism A prism is a polyhedron with two parallel, congruent bases. The other faces, also called lateral faces , are rectangles. triangular prism octagonal prism 3.1.1b Pyramid A pyramid is a polyhedron with one base and the lateral sides ( all are triangular sides ) meet at a common vertex. hexagonal pyramid square pyramid. Example 1: Determine if the following solids are polyhedrons. If the solid is a polyhedron, name it and find the number of faces, vertices and edges each has. a) b) c) Solution: a) The base is a triangle and all the sides are triangles, so this is a polyhedron. It is called triangular pyramid. There are 4 faces, 4 vertices and 6 edges. b) This solid is also a polyhedron because all faces are polygons. The bases are both pentagons, so it is a pentagonal prism. There are 7 faces, 10 vertices, and 15 edges.
c) This is a cylinder and has bases that are circles. Circles are not polygons, so it is not a polyhedron. 3.1.2 Eulerโs Theorem Letโs put our results from Example 1 into a table. Faces Vertices Edges Triangular Pyramid 4 4 6 Pentagonal Prism 7 10 15 Notice that faces + vertices is two more that the number of edges. This is called Eulerโs Theorem , after the Swiss mathematician Leonhard Euler. Eulerโs Formula for Polyhedra: this can be used to find the number of vertices (V), faces (F), or edges (E) on a polyhedron: ๐ + ๐ = ๐ + ๐ If a figure does not satisfy Eulerโs formula, the figure is not a polyhedron. Illustration: ๐๐ซ๐๐ฐ ๐ + ๐๐ฐ ๐๐ฑ ๐๐๐ฐ ๐ = ๐๐ซ๐๐ฐ ๐ + ๐ ๐ + ๐ = ๐ + ๐ Example 2: Find the number of faces, vertices, and edges in the octagonal prism. Solution: There are 10 faces and 16 vertices. Use Eulerโs Theorem, to solve for E. ๐ + ๐ = ๐ + ๐ 10 + 16 = ๐ + 2 ๐๔ = ๐
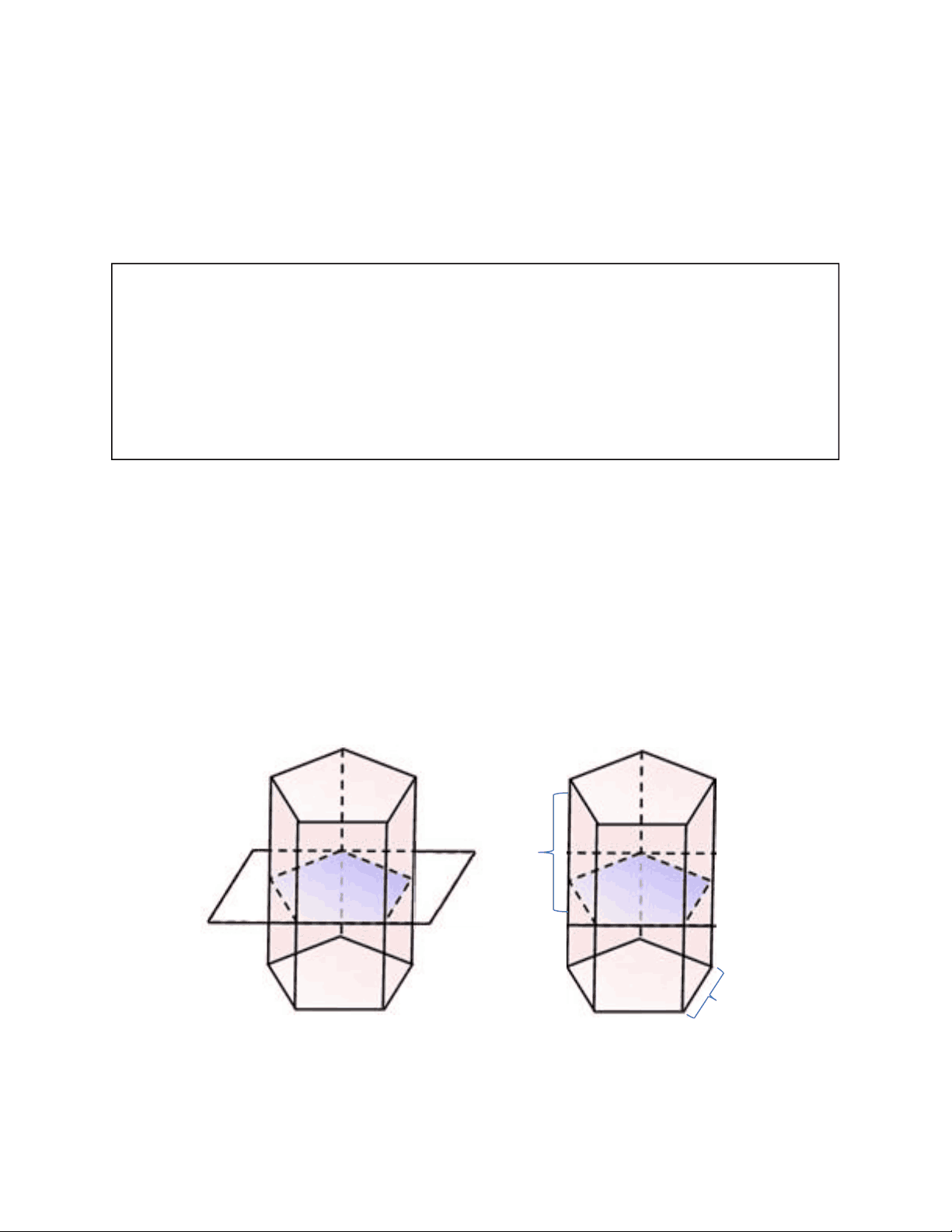
Regular Dodecahedron: A 12-faced polyhedron and all the faces are regular pentagons. Regular Icosahedron: A 20-faced polyhedron and all the faces are equilateral triangles. 3.1.4 Cross-Sections One way to โviewโ a three-dimensional figure in a two-dimensional plane is to use cross- sections. A cross-section is the intersection of a plane with a solid. Illustration: The cross-section of the peach plane and the tetrahedron is a triangle. Example 5: What is the shape formed by the intersection of the plane and the regular octahedron? a) b) c) Solution: a) Square b) Rhombus c) Hexagon
3.1. Nets A net is an unfolded, flat representation of the sides of a three-dimensional shape. Illustration: Example 6: What kind of figure does this net create? Solution: Example 7: Draw a net of the right triangular prism below. Solution: The net will have two triangles and three rectangles. The rectangles are different sizes and the two triangles are the same. Note: There are several different nets of any polyhedron. For example, this net could have the triangles anywhere along the top or bottom of the three rectangles. ๏ถ Know What? Revisited ( first page ) The net of the shape is a regular tetrahedron.
