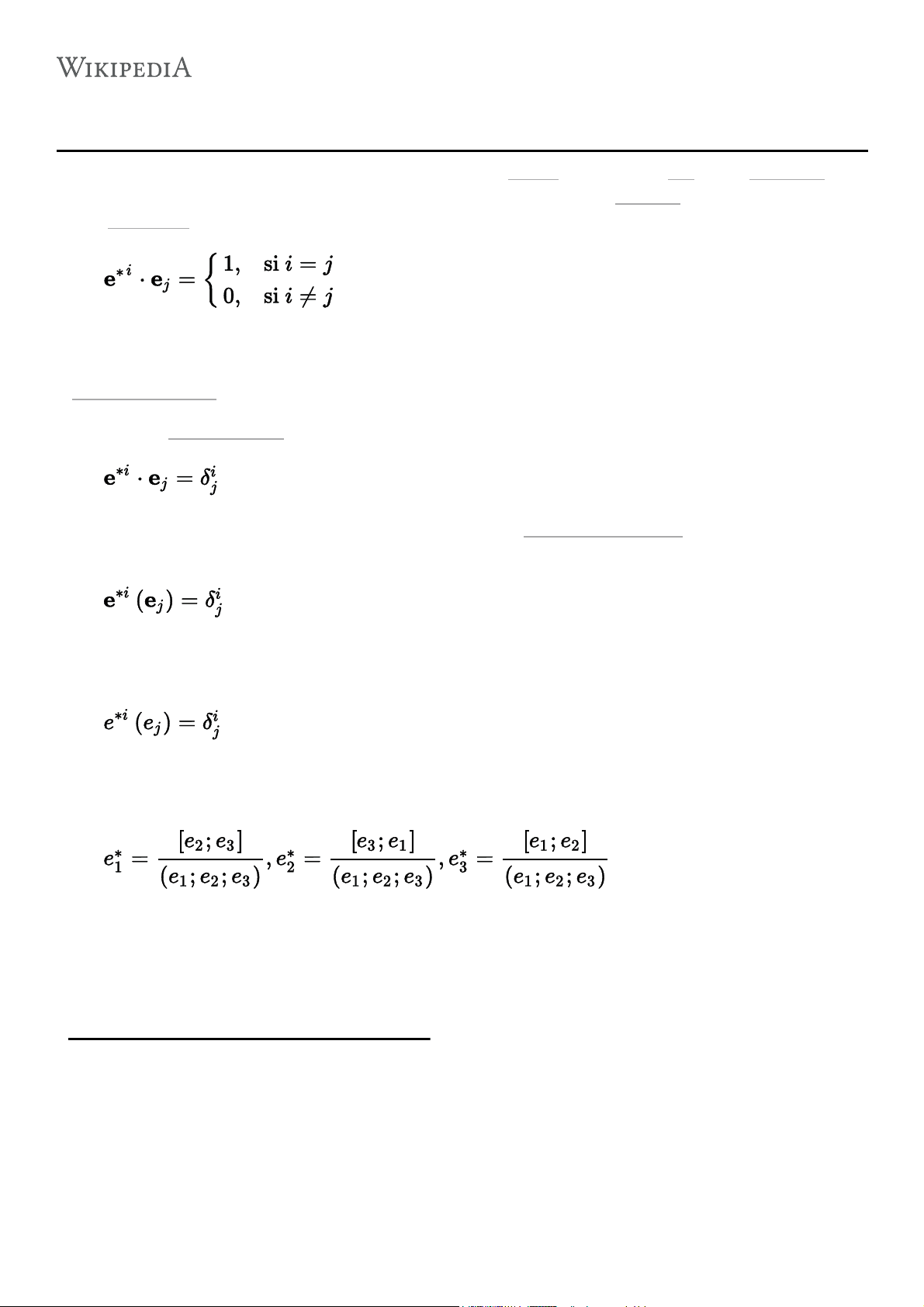




Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Base dual en geometría diferencial. Base recíproca
Typology: Exercises
1 / 4

This page cannot be seen from the preview
Don't miss anything!
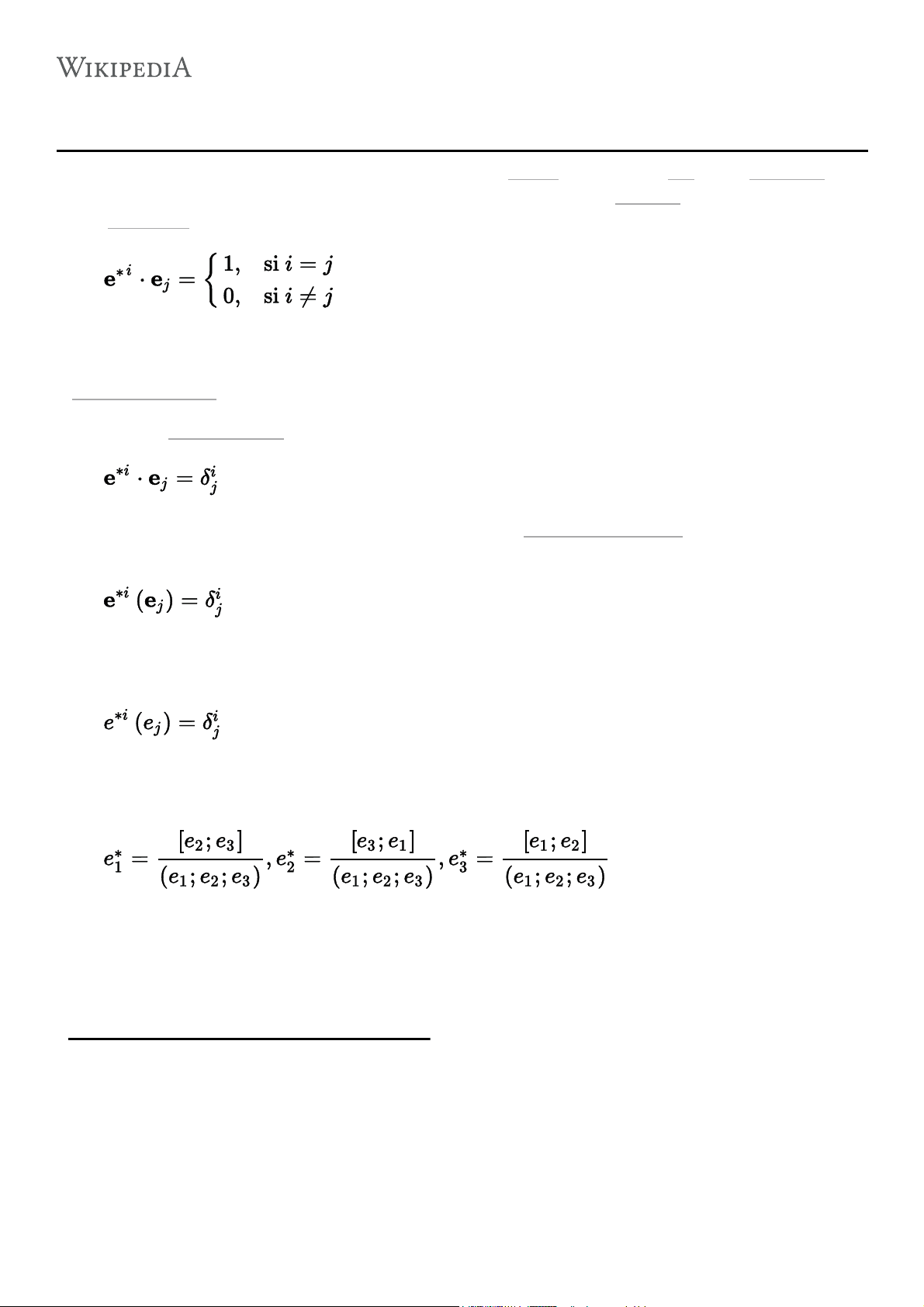


En álgebra lineal, una base dual o base biortogonal es un conjunto de vectores que forman una base para el espacio dual de un espacio vectorial. Para un espacio vectorial V de dimensiones finitas, el espacio dual V * es isomórfico a V y para cualquier conjunto dado de vectores base { e 1 , …, e n} de V , hay asociada una base dual { e^1 ,..., e n} de V * con la relación
Concretamente, podemos escribir vectores en un espacio vectorial V de n dimensiones como una matriz de columna de n × 1 dimensiones y los elementos del espacio dual V * como matrices de fila de 1 × n que actúan como funcionales lineales por medio de la multiplicación matriciala la izquierda.
También se usa la delta de Kronecker como nomenclatura para la definición anterior como sigue
Y en muchos textos de álgebra lineal también es común representar el producto punto o interno de dos vectores únicamente encerrando en un paréntesis el segundo vector como sigue
Así como asumir que son vectores sin usar negritas, debido ya sea a que están en un producto punto o a que no tienen subíndices o superíndices como sigue:
Para el caso de un espacio tridimensional, teniendo una base dada e , se puede encontrar la base biortogonal (dual) por medio de estas fórmulas:
Cuyo uso se aclara mejor con el siguiente ejemplo.
1 Ejemplo 2 Propiedades de la base dual 2.1 Efecto en un vector 2.2 Coordenadas respecto a la base dual 3 Véase también 4 Enlaces externos
Encontrar la base dual para un espacio en R^3 cuyas bases están dadas por:
Calculamos la base dual para su espacio dual
para comprobar que nuestro resultado está bien, usamos la condición
que es equivalente en este caso a
al sustituir se obtiene
Cada transformación lineal F en V *^ puede ser expresada únicamente como una combinación lineal de la transformación e i^ y por eso:
( e 1, ..., e _n_ ) es efectivamente una base de V *, que es por lo tanto de dimensión n ; la fi es el vector de coordenadasde F con respecto a tal base.
Espacio dual
Weisstein, Eric W. «DualBasis». En Weisstein, Eric W. MathWorld (en inglés). Wolfram Research.
Obtenido de «https://es.wikipedia.org/w/index.php?title=Base_dual&oldid=100212863»
Se editó esta página por última vez el 2 jul 2017 a las 10:35.
El texto está disponible bajo laLicencia Creative Commons Atribución Compartir Igual 3.0; pueden aplicarse cláusulas adicionales. Al usar este sitio, usted acepta nuestrostérminos de uso y nuestra política de privacidad. Wikipedia® es una marca registrada de laFundación Wikimedia, Inc., una organización sin ánimo de lucro.