






Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
These are the Lecture Slides of Algorithms and Applications in Java which includes Greedy Method, Divide and Conquer, Dynamic Programming, Backtracking, Branch and Bound, Integer Programming, Neural Networks, Genetic Algorithms, Tabu Search etc.Key important points are: Backtracking, Branch and Bound, Subset Problem, Permutation Problems, Tree Organization, Solution Space, Subset Tree, Permutation Tree, Depth-First Manner, Bounding Functions, Subet Sum
Typology: Slides
1 / 16

This page cannot be seen from the preview
Don't miss anything!










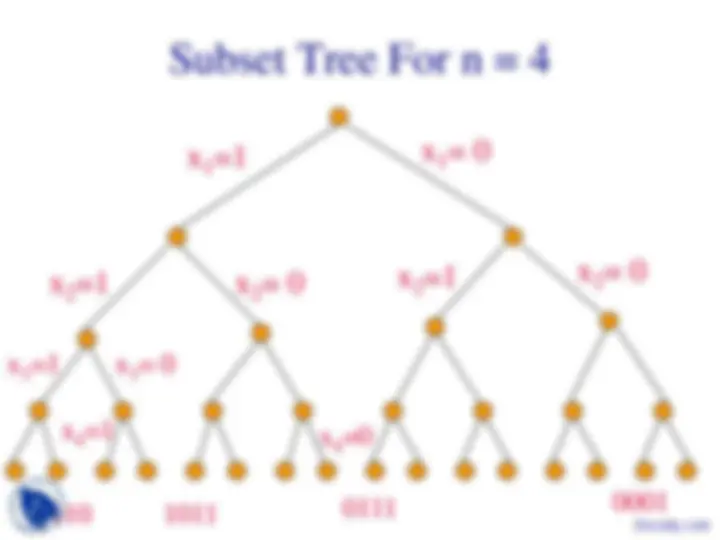
Nonsystematic search of the space for the answer takes O(p2 n^ ) time, where p is the time needed to evaluate each member of the solution space.
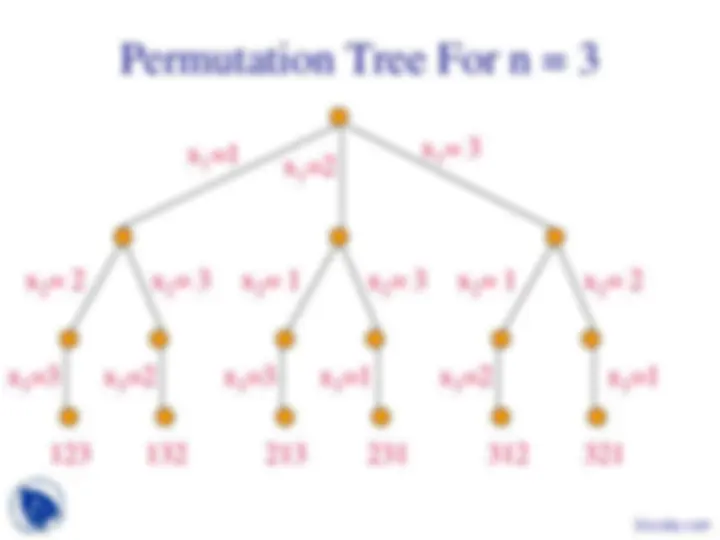
Nonsystematic search of the space for the answer takes O(pn!) time, where p is the time needed to evaluate each member of the solution space.
- Subset Tree For n = - x 1 =1 x^1 = x 1 =1 (^) x 1 =^
x 1 = 3
x 2 = 2 x 2 = 3 x 2 = 1 x 2 = 3 x 2 = 1 x 2 = 2
x 3 =3 x 3 =2 x 3 =3 x 3 =1 x 3 =2 x 3 =
123 132 213 231 312 321
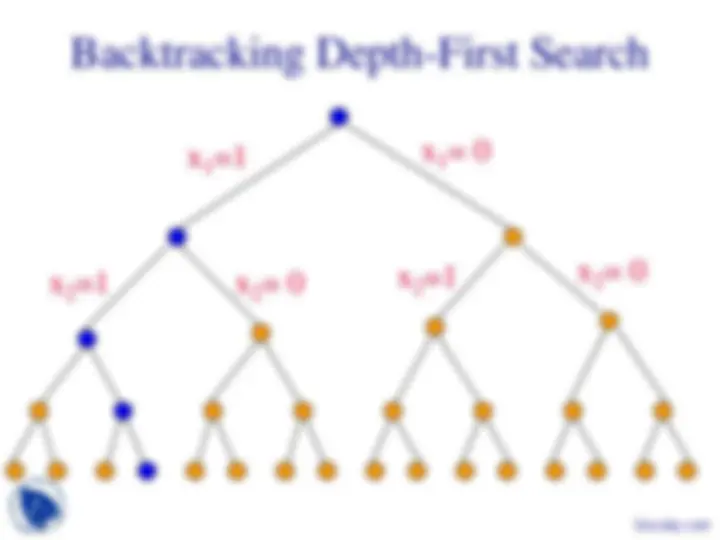
x 1 =1 x^1 = 0
x 2 =1 x 2 = 0 x^2 =1^ x^2 = 0
x 1 =1 x^1 = 0
x 2 =1 x 2 = 0 x^2 =1^ x^2 = 0
x 1 =1 x^1 = 0
x 2 =1 x 2 = 0 x^2 =1^ x^2 = 0
x 1 =1 x^1 = 0
x 2 =1 x 2 = 0 x^2 =1^ x^2 = 0
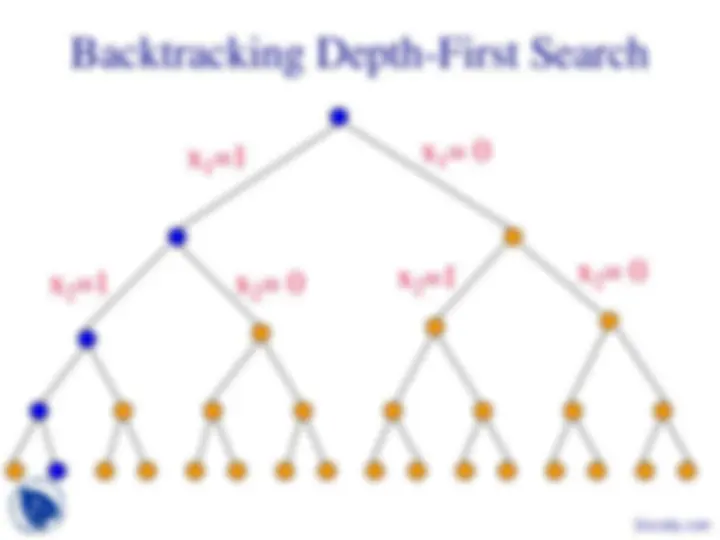
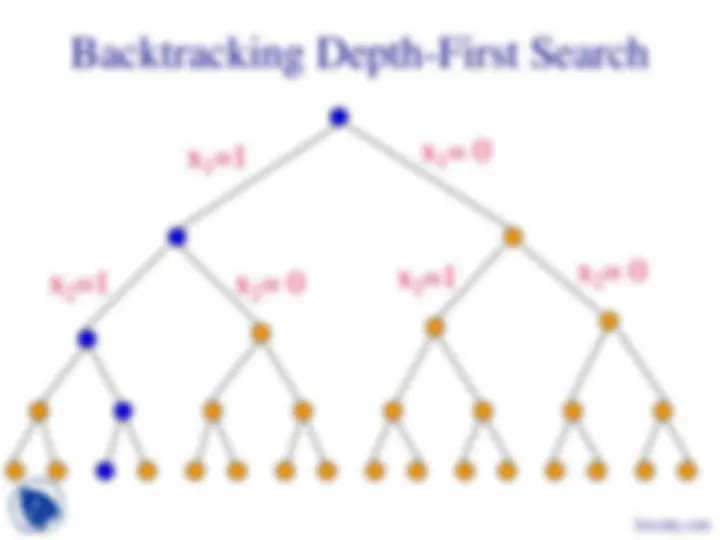
FIFO branch and bound finds solution closest to root. Backtracking may never find a solution because tree depth is infinite (unless repeating configurations are eliminated).