Download All-Pairs Shortest Paths Algorithms: Dijkstra, Floyd-Warshall, and Decision Sequence and more Slides Computer Science in PDF only on Docsity!
All-Pairs Shortest Paths
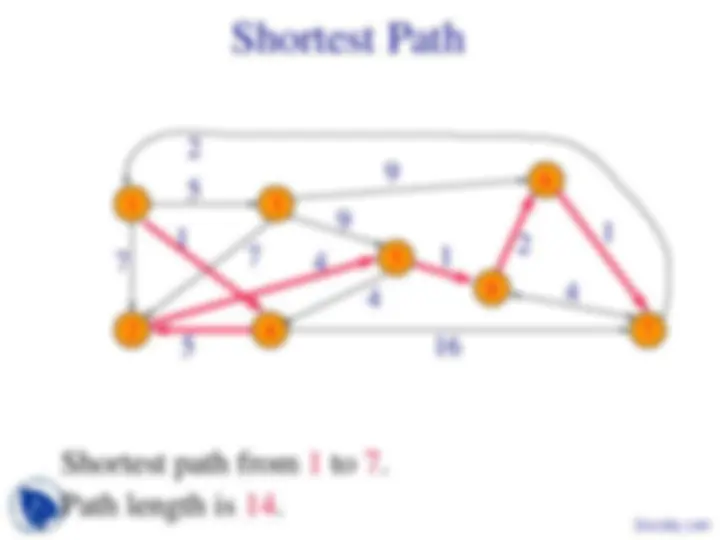
- Given an n-vertex directed weighted graph, find a shortest path from vertex i to vertex j for each of the n 2 vertex pairs (i,j).
1
2
3
4
5
6
7
5
7
(^1 )
9
1
9 4 4 5 16
4
2
8
2 1
Dijkstra’s Single Source Algorithm
- Use Dijkstra’s algorithm n times, once with each of the n vertices as the source vertex.
1
2
3
4
5
6
7
5
7
(^1 )
9
1
9 4 4 5 16
4
2
8
2 1
Dynamic Programming Solution
- Time complexity is Theta(n^3 ) time.
- Works so long as there is no cycle whose length is < 0.
- When there is a cycle whose length is < 0, some shortest paths aren’t finite. If vertex 1 is on a cycle whose length is -2, each time you go around this cycle once you get a 1 to 1 path that is 2 units shorter than the previous one.
- Simpler to code, smaller overheads.
- Known as Floyd’s shortest paths algorithm.
Decision Sequence
- First decide the highest intermediate vertex (i.e., largest vertex number) on the shortest path from i to j.
- If the shortest path is i, 2, 6, 3, 8, 5, 7, j the first decision is that vertex 8 is an intermediate vertex on the shortest path and no intermediate vertex is larger than 8.
- Then decide the highest intermediate vertex on the path from i to 8, and so on.
i j
Cost Function
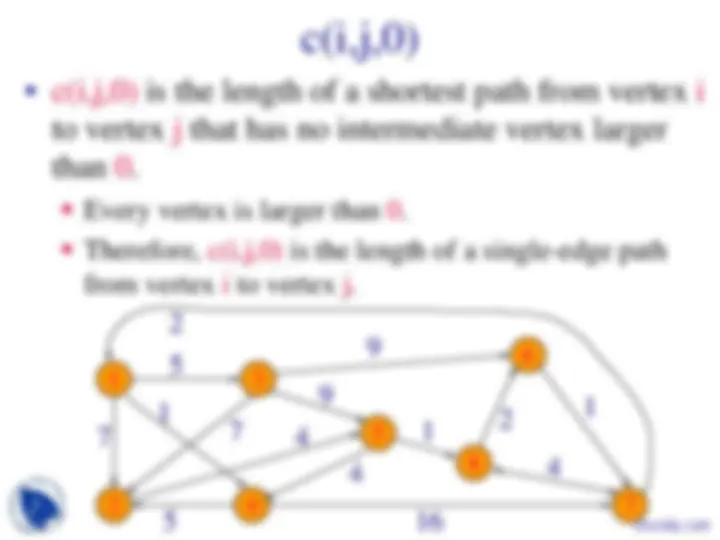
- Let c(i,j,k) be the length of a shortest path from vertex i to vertex j that has no intermediate vertex larger than k.
i j
c(i,j,n)
- c(i,j,n) is the length of a shortest path from vertex i to vertex j that has no intermediate vertex larger than n.
- No vertex is larger than n.
- Therefore, c(i,j,n) is the length of a shortest path from vertex i to vertex j.
1
2
3
4
5
6
7
5
7
(^1 )
9
1
9 4 4 4
2
8
2 1
Recurrence For c(i,j,k), k > 0
- The shortest path from vertex i to vertex j that has no intermediate vertex larger than k may or may not go through vertex k.
- If this shortest path does not go through vertex k, the largest permissible intermediate vertex is k-1. So the path length is c(i,j,k-1).
i j
< k
Recurrence For c(i,j,k) ), k > 0
- Shortest path goes through vertex k.
i j
k
- We may assume that vertex k is not repeated because no cycle has negative length.
- Largest permissible intermediate vertex on i to k and k to j paths is k-1.
Recurrence For c(i,j,k) ), k > 0
i j
k
- Similarly, k to j path must be a shortest k to j path that goes through no vertex larger than k-1.
- Therefore, length of i to k path is c(i,k,k-1), and length of k to j path is c(k,j,k-1).
- So, c(i,j,k) = c(i,k,k-1) + c(k,j,k-1).
Recurrence For c(i,j,k) ), k > 0
- Combining the two equations for c(i,j,k), we get c(i,j,k) = min{c(i,j,k-1), c(i,k,k-1) + c(k,j,k-1)}.
- We may compute the c(i,j,k)s in the order k = 1, 2, 3, …, n.
i j
Space Reduction
- c(i,j,k) = min{c(i,j,k-1), c(i,k,k-1) + c(k,j,k-1)}
- When neither i nor j equals k, c(i,j,k-1) is used only in the computation of c(i,j,k). column k
row k
(i,j)
- So c(i,j,k) can overwrite c(i,j,k-1).
Space Reduction
- c(i,j,k) = min{c(i,j,k-1), c(i,k,k-1) + c(k,j,k-1)}
- When i equals k, c(i,j,k-1) equals c(i,j,k).
c(k,j,k) = min{c(k,j,k-1), c(k,k,k-1) + c(k,j,k-1)} = min{c(k,j,k-1), 0 + c(k,j,k-1)} = c(k,j,k-1)
- So, when i equals k, c(i,j,k) can overwrite c(i,j,k-1).
- Similarly when j equals k, c(i,j,k) can overwrite c(i,j,k-1).
- So, in all cases c(i,j,k) can overwrite c(i,j,k-1).Docsity.com
Building The Shortest Paths
- Let kay(i,j) be the largest vertex on the shortest path from i to j.
- Initially, kay(i,j) = 0 (shortest path has no intermediate vertex).
for (int k = 1; k <= n; k++) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) if (c(i,j) > c(i,k) + c(k,j)) {kay(i,j) = k; c(i,j) = c(i,k) + c(k,j);}
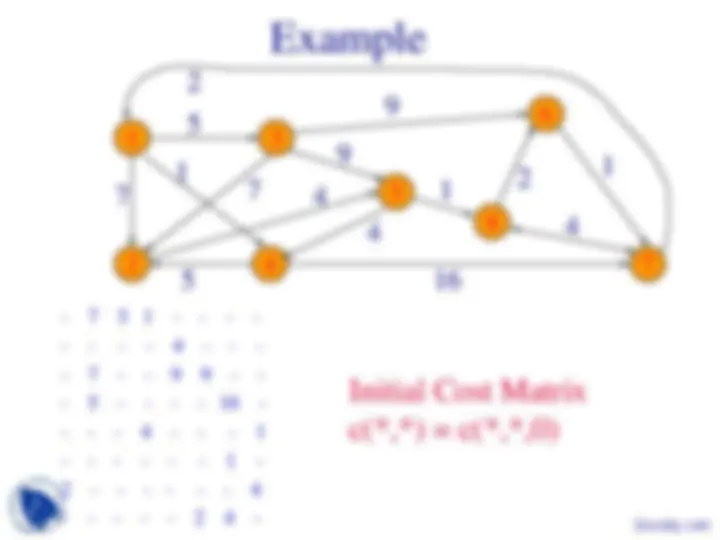
Example
- 7 5 1 - - - -
- 7 - - 9 9 - -
- 5 - - - - 16 -
1
2
3
4
5
6
7
5
7
(^1 )
9
1
9 4 4 5 16
4
2
8
2 1
Initial Cost Matrix c(,) = c(,,0)